Significado
Cientistas e gerentes têm se preocupado com a questão de saber se e, em caso afirmativo, sob quais condições grupos de solucionadores de problemas em interação superam indivíduos autônomos. Aqui descrevemos um experimento no qual indivíduos e grupos foram avaliados em uma série de tarefas de complexidade variável. Descobrimos que os grupos são tão rápidos quanto o indivíduo mais rápido e mais eficientes do que o indivíduo mais eficiente quando a tarefa é complexa, mas não quando a tarefa é simples. Em seguida, quantificamos com precisão os ganhos sinérgicos e as perdas de processo associadas aos grupos interativos, descobrindo que o equilíbrio entre os dois depende da complexidade. Nosso estudo tem o potencial de reconciliar descobertas conflitantes sobre sinergia de grupo em trabalhos anteriores.
Resumo
A complexidade—definida em termos do número de componentes e a natureza das interdependências entre eles—é claramente uma característica relevante de todas as tarefas que os grupos executam. No entanto, o papel que a complexidade da tarefa desempenha na determinação do desempenho do grupo permanece pouco compreendido, em parte porque não existe uma linguagem clara para expressar a complexidade de uma forma que permita comparações diretas entre as tarefas. Aqui evitamos essa dificuldade analítica identificando uma classe de tarefas para as quais a complexidade pode ser variada sistematicamente, mantendo todos os outros elementos da tarefa inalterados. Em seguida, testamos os efeitos da complexidade da tarefa em um experimento de duas fases pré-registrado no qual 1.200 indivíduos foram avaliados em uma série de tarefas de complexidade variável (fase 1) e, em seguida, designados aleatoriamente para resolver tarefas semelhantes em grupos de interação ou como indivíduos independentes ( fase 2). Descobrimos que os grupos de interação são tão rápidos quanto o indivíduo mais rápido e mais eficientes do que o indivíduo mais eficiente para tarefas complexas, mas não para tarefas mais simples. Aproveitando nossos dados digitais altamente granulares, definimos e medimos com precisão as perdas de processo de grupo e os ganhos sinérgicos e mostramos que o equilíbrio entre os dois interruptores indica valores intermediários de complexidade da tarefa. Finalmente, descobrimos que os grupos interativos geram mais soluções mais rapidamente e exploram o espaço de soluções de forma mais ampla do que os solucionadores de problemas independentes, encontrando soluções de maior qualidade do que todos, exceto os indivíduos com pontuação mais alta.
Tarefas executadas por grupos de solucionadores de problemas interativos - seja no mundo real ou em configurações experimentais - variam em várias dimensões que influenciam plausivelmente o desempenho do grupo (1⇓⇓⇓⇓–6). Neste artigo, focamos em uma dimensão importante, mas pouco estudada empiricamente, das tarefas, a complexidade, que geralmente é entendida como dependente de pelo menos dois fatores: (i) o número de componentes distintos que constituem uma tarefa e (ii) o número, força , e configuração de interdependências entre esses componentes (7⇓⇓⇓–11).
Intuitivamente, a complexidade da tarefa é de relevância óbvia para o desempenho do grupo. Com tudo o mais igual, seria de esperar que os solucionadores de problemas tivessem um desempenho pior em tarefas que tivessem mais componentes ou para as quais as interações entre os componentes fossem mais densas. Além disso, pode-se também esperar que a complexidade da tarefa afete a “sinergia” do grupo, definida como desempenho superior ao que seria esperado para uma coleção de tamanho semelhante de indivíduos trabalhando de forma independente – também conhecido como “grupo nominal” (12). Nesse caso, entretanto, é menos óbvio qual seria a direção do efeito. Por um lado, os grupos interativos podem ter um desempenho melhor em relação aos grupos nominais em tarefas complexas porque são capazes de distribuir esforços (13), compartilhar informações sobre soluções de alta qualidade (14) ou corrigir erros (15). Por outro lado, com tarefas mais complexas, os grupos de interação podem experimentar perdas de processo ainda maiores - incluindo vadiagem social (16), pensamento de grupo (17) e conflito interpessoal (4) - possivelmente porque tarefas complexas exigem mais dos colaboradores individuais e oferecem mais oportunidades para ficar preso em ótimos locais subótimos globalmente, qualquer um dos quais também pode levar a aumento de estresse e baixo desempenho em relação a grupos nominais.
Um grande desafio para resolver questões sobre os efeitos da complexidade da tarefa é que, embora o conceito de alto nível pareça intuitivo, ainda não foi operacionalizado com precisão suficiente para permitir que os pesquisadores quantifiquem a complexidade de diferentes tipos de tarefas e, portanto, façam maçãs a comparações de maçãs entre eles. Em vez disso, as operacionalizações existentes são muitas vezes complexas. Por exemplo, um modelo lista 27 fatores que contribuem para a complexidade agrupados em 10 dimensões de complexidade (9), enquanto outros modelos são suficientemente específicos do domínio para que as diferenças numéricas entre diferentes tipos de tarefas sejam difíceis de interpretar (7). Para aumentar a confusão, algumas definições enfatizam a complexidade objetiva, referindo-se apenas aos recursos da tarefa que podem ser medidos independentemente de quem a executa, enquanto outras enfatizam a complexidade subjetiva, a complexidade da tarefa conforme experimentada por quem a executa (9, 11).
Aqui evitamos essas dificuldades analíticas identificando uma classe de tarefas para as quais a complexidade pode ser variada sistematicamente, mantendo todos os outros elementos da tarefa fixos. Dessa forma, podemos facilmente medir o desempenho em função do aumento da complexidade sem nos preocuparmos com confusões decorrentes de outros aspectos da tarefa, como o tipo de tarefa (3) ou outras características dos processos de grupo (4, 18). Além disso, exigimos que nossas tarefas possam ser realizadas de forma realista, de forma independente ou colaborativa, permitindo assim uma comparação direta entre grupos nominais e de interação.
Uma classe de tarefas que satisfazem esses critérios são os problemas de satisfação e otimização de restrições (CSOPs), que são amplamente estudados em inteligência artificial e pesquisa de operações. A conexão com a pesquisa operacional é útil porque, ao contrário de outros problemas de “brinquedos”, os CSOPs mapeiam de maneira relativamente intuitiva uma variedade de problemas práticos de alocação de recursos e têm sido usados para modelar muitos problemas de interesse prático. Exemplos de CSOPs incluem projetos de software de pessoal onde há várias designações potenciais de desenvolvedor para atividade a serem avaliadas (19); formar grupos de aprendizagem com base em alguns critérios relacionados aos objetivos da colaboração (20); horários ferroviários (21); e alocação de vacinas, ventiladores e suprimentos médicos durante a pandemia de COVID-19 (22). Além disso, embora os CSOPs capturem características importantes dos exercícios de resolução de problemas em grupo do mundo real, eles não exigem que os participantes tenham habilidades especializadas. Como resultado, os participantes podem ser recrutados a partir de serviços online, reduzindo o custo e a dificuldade de coordenar a participação simultânea dos grupos. Finalmente, como em outros problemas complexos (14, 23⇓–25), a função de recompensa para CSOPs pode ser descrita como uma paisagem de desempenho robusta, onde cada ponto na paisagem representa uma combinação de escolhas potencialmente interdependentes (uma solução para o problema). , enquanto a altura do ponto representa o desempenho dessa combinação (26, 27). Portanto, os CSOPs podem ser caracterizados por várias soluções localmente ótimas, mas globalmente subótimas (26, 27) e, portanto, são passíveis de potencialmente muitas estratégias e estilos de solução, sem uma única estratégia universalmente superior (28).
O CSOP específico que estudamos é um problema de alocação de salas no qual os participantes - individualmente ou em grupos - designam N alunos para M salas onde cada aluno tem uma utilidade específica para cada sala (SI Apêndice, seção 1.1). O objetivo da tarefa é maximizar a utilidade total do aluno, respeitando também as restrições Q (por exemplo, “Os alunos A e J não podem dividir um quarto ou estar em quartos adjacentes”). Quando a tarefa é realizada em grupos, os participantes podem se comunicar por meio de bate-papo baseado em texto e mover diferentes alunos simultaneamente, realizando processamento paralelo, se assim o desejarem. De forma crítica para nossos propósitos, a complexidade da tarefa pode ser variada sistematicamente ajustando apenas três parâmetros principais: o número de alunos , o número de salas e o número de restrições . De fato, uma vantagem significativa desta tarefa (e CSOPs em geral) sobre tarefas que são mais comumente estudadas em configurações de desempenho de grupo é que sua complexidade pode ser quantificada em termos do tempo de execução exigido por um solucionador algorítmico para encontrar a solução ótima, permitindo para classificar facilmente as instâncias de tarefas por complexidade (consulte Materiais e métodos para obter mais detalhes). A Fig. 1 ilustra como a complexidade pode variar entre duas instâncias do problema de alocação de salas. Em uma instância de baixa complexidade, seis alunos devem ser alocados em quatro quartos sujeitos a apenas duas restrições (“B e E devem ser vizinhos” e “C e F não podem morar no mesmo quarto”). Em uma instância de alta complexidade, 18 alunos devem ser alocados em 8 salas sujeitas a 18 restrições.
Ilustração da tarefa de atribuição de quartos. A tarefa exigia atribuir N alunos a M salas de modo a maximizar a utilidade total dos alunos, cada um com uma utilidade específica para cada sala, respeitando também as restrições Q. A complexidade da tarefa é caracterizada pelo número de alunos a serem atribuídos , o número de dormitórios disponíveis e o número de restrições . (Topo) Um caso de baixa complexidade em que seis alunos devem ser alocados em quatro salas sujeitas a duas restrições. (Abaixo) Um caso de alta complexidade no qual 18 alunos serão distribuídos em 8 salas sujeitas a 18 restrições. Veja o Apêndice SI, seção S1.1, para detalhes e o Apêndice SI, Figs. S1–S2, para capturas de tela da interface de tarefas.
Projeto de experimento
Neste artigo, testamos a hipótese de que a complexidade da tarefa modera o desempenho relativo da resolução de problemas em grupo versus individual. Para tanto, abordamos a seguinte questão: como o equilíbrio entre perdas de processo e ganhos sinérgicos em grupos em interação depende da complexidade da tarefa?
Nosso experimento ocorreu em duas fases. Na fase 1, 1.200 participantes completaram individualmente cinco tarefas de atribuição de sala: três tarefas de complexidade muito baixa e duas de complexidade moderada (SI Apêndice, Tabela S1), bem como um teste padrão de Ler a Mente nos Olhos (SI Apêndice, seção S1.2 e Fig. S3), que é comumente usado como uma medida de percepção social e foi usado por vários estudos recentes relacionando a percepção social ao desempenho do grupo (18, 29⇓⇓–32).
Após a conclusão da fase 1, avaliamos todos os participantes em nível de habilidade e percepção social para que pudéssemos atribuí-los aos blocos experimentais na fase 2 (SI Apêndice, seção 1.4 e Fig. S4). Levando em conta essas características em nosso procedimento de randomização em bloco na fase 2, pudemos garantir que vários níveis de habilidade e percepção social (e suas combinações) fossem equilibrados entre os arranjos de trabalho em grupo e individual. O principal objetivo do esquema de randomização em bloco era superamostrar combinações estatisticamente menos frequentes (por exemplo, todos os membros do grupo com altas habilidades ou alta percepção social), aumentando assim o poder estatístico de nossos experimentos. Observamos que nosso foco aqui está na comparação entre grupos nominais e interativos, não nas diferenças de composição entre grupos interativos; assim, nossa análise dos efeitos do nível de habilidade e percepção social sobre o desempenho será publicada em outro lugar (conforme nosso pré-registro).
Os mesmos 1.200 participantes foram convidados a participar da fase 2, e os primeiros 828 participantes que apareceram e passaram nas verificações de atenção (conforme nosso pré-registro; consulte o Apêndice SI, Tabela S2, para tamanhos de amostra) foram designados para um segundo sequência de cinco tarefas de atribuição de sala (a sequência de tarefas foi aleatória), também de complexidade variável (muito baixa, baixa, moderada, alta e muito alta; Apêndice SI, Tabela S3 e Fig. S5). Todas as tarefas expiraram em 10 min na fase 2, independentemente da complexidade. Com base na habilidade de cada participante e na percepção social medida na fase 1, primeiro atribuímos cada indivíduo em blocos (por exemplo, alta habilidade, alta percepção social; habilidade mista, alta percepção social; etc.). Em seguida, dentro de cada bloco, os participantes foram randomizados para uma das duas condições: uma condição de grupo interativo ( participantes, formando 197 grupos de tamanho 3; dados para 1 grupo estão incompletos, levando ao número de grupos de interação válidos sendo 196), nos quais os membros do grupo resolviam o problema coletivamente e podiam se comunicar uns com os outros via chat baseado em texto; e uma condição individual independente ( participantes; os dados de 3 indivíduos estão incompletos, levando ao número de indivíduos independentes válidos sendo 234), em que cada participante trabalhou sozinho em sua tarefa atribuída. Todos os resultados aqui apresentados são da fase 2 do experimento.
Avaliação de desempenho.
Na fase 2, usamos três métricas para capturar o desempenho em uma instância de tarefa de atribuição de sala: (1) pontuação normalizada, definida como a pontuação real obtida em uma instância de tarefa dividida pela pontuação máxima possível para essa tarefa; (2) duração (ou tempo para conclusão), definida como o tempo decorrido desde o início da tarefa até a apresentação de uma solução (ou até que a tarefa expire em 10 min); e, finalmente, (3) eficiência, definida como a pontuação normalizada dividida pela duração.
Todas as três métricas são indicadores naturais de desempenho que podem ser otimizados em algumas circunstâncias. Na ausência de restrições de tempo, por exemplo, a pontuação normalizada é uma medida óbvia da qualidade da solução. Por outro lado, a duração é apropriada quando o tempo de resolução de problemas é mais importante do que a qualidade (por exemplo, crie rapidamente um plano razoavelmente bom para alocação de recursos em uma resposta a desastres) e a eficiência é apropriada quando a qualidade e a velocidade são importantes (por exemplo, , no desenvolvimento de produtos).
Seguindo trabalhos anteriores (12, 33⇓⇓⇓–37), avaliamos o desempenho do grupo em comparação com os chamados grupos nominais, definidos como uma coleção de indivíduos autônomos de tamanho semelhante. Grupos nominais fornecem uma referência útil para grupos de interação porque eles respondem pela disponibilidade de recursos diferenciais entre grupos e indivíduos (12); ou seja, eles ajustam a quantidade de recursos intelectuais que os grupos poderiam empregar (ou seja, horas de trabalho) e a probabilidade matemática de que pelo menos um membro pudesse ter alcançado o mesmo desempenho. Assim, o desempenho do grupo interativo acima e acima de um grupo nominal pode ser atribuído à interação do grupo, não a maiores recursos.
Em geral, as comparações entre grupos de interação e grupos nominais de tamanho equivalente encontraram evidências mistas de efeitos sinérgicos (12): enquanto os grupos de interação geralmente superam o membro médio de um grupo nominal (sinergia fraca), eles raramente superam o melhor membro ( forte sinergia). Refletindo essa distinção, comparamos nossos grupos de interação com quatro benchmarks de desempenho, cada um correspondendo a um grupo nominal distinto construído por sorteio de três indivíduos aleatoriamente e sem reposição do mesmo bloco. O primeiro benchmark corresponde à pontuação de desempenho para um membro escolhido aleatoriamente do grupo nominal (equivalente a um indivíduo médio), enquanto os três restantes correspondem ao indivíduo com o melhor desempenho da fase 1 em cada uma das três métricas definidas acima (ou seja, maior pontuação, menor duração e maior eficiência). Grupos nominais, portanto, simulam uma situação na qual um gerente atribui o trabalho a um indivíduo aleatório, o indivíduo com maior pontuação, o indivíduo mais rápido ou o indivíduo mais eficiente, conforme julgado pelo desempenho passado (ou seja, pontuações da fase 1, durações e eficiência).
Resultados
Desempenho em função da complexidade da tarefa.
Fig. 2 mostra como o desempenho variou em função da complexidade da tarefa. Em todas as condições, a maior complexidade da tarefa resultou em pontuações normalizadas mais baixas (Fig. 2A), maior duração (Fig. 2B) e, portanto, menor eficiência (Fig. 2C). Essas tendências de desempenho também são válidas quando medidas separadamente para grupos nominais e interativos (SI Apêndice, seção S2 e Fig. S7). Em média, indivíduos e grupos gastaram cerca de três vezes mais tempo na tarefa mais complexa do que na tarefa menos complexa, mas obtiveram pontuações normalizadas que foram aproximadamente 10 pontos percentuais menores. Dado que as pontuações normalizadas foram quase sempre superiores a 80, essa última diferença representa aproximadamente 50% da faixa efetiva - um grande efeito. A clara dependência monotônica de todas as três medidas de desempenho em relação à complexidade é importante por dois motivos. Em primeiro lugar, ele valida nosso projeto, demonstrando que os aumentos na complexidade capturados pelas mudanças nos parâmetros da tarefa N, M e Q se traduzem de maneira direta na complexidade experimentada por nossos participantes. Em segundo lugar, oferece uma alavancagem considerável para testar nossa previsão de que o desempenho relativo de grupos interativos versus grupos nominais depende da complexidade da tarefa.
Variar a complexidade da tarefa de atribuição de quartos. Aumentar a complexidade da tarefa (A) reduz a pontuação normalizada, (B) aumenta o tempo necessário para concluir a tarefa e (C) reduz a eficiência. Os dados são combinados em condições individuais e de grupo em todos os seis blocos. As barras de erro indicam os intervalos de confiança de 95% (alguns não são grandes o suficiente para serem exibidos). Grupos e indivíduos acertaram pelo menos 80% da pontuação máxima em mais de 85% das tarefas; portanto, a faixa efetiva para a pontuação normalizada (ou seja, o eixo y de A) está entre 80 e 100%. O tempo mínimo necessário para a apresentação de uma solução é de 1 min e o máximo é de 10 min; portanto, a faixa efetiva para a duração (ou seja, o eixo y de B) está entre 1 e 10 min. A diferença na dificuldade experimentada entre complexidade muito baixa e muito alta é muito grande: a pontuação média normalizada caiu cerca de 50% da faixa efetiva de pontuações (de aproximadamente 95 a 85% em uma escala efetiva de 80 a 100) e a o tempo médio gasto aumentou em 200% (de 2 para 6 min).
Evidência para sinergia de grupo.
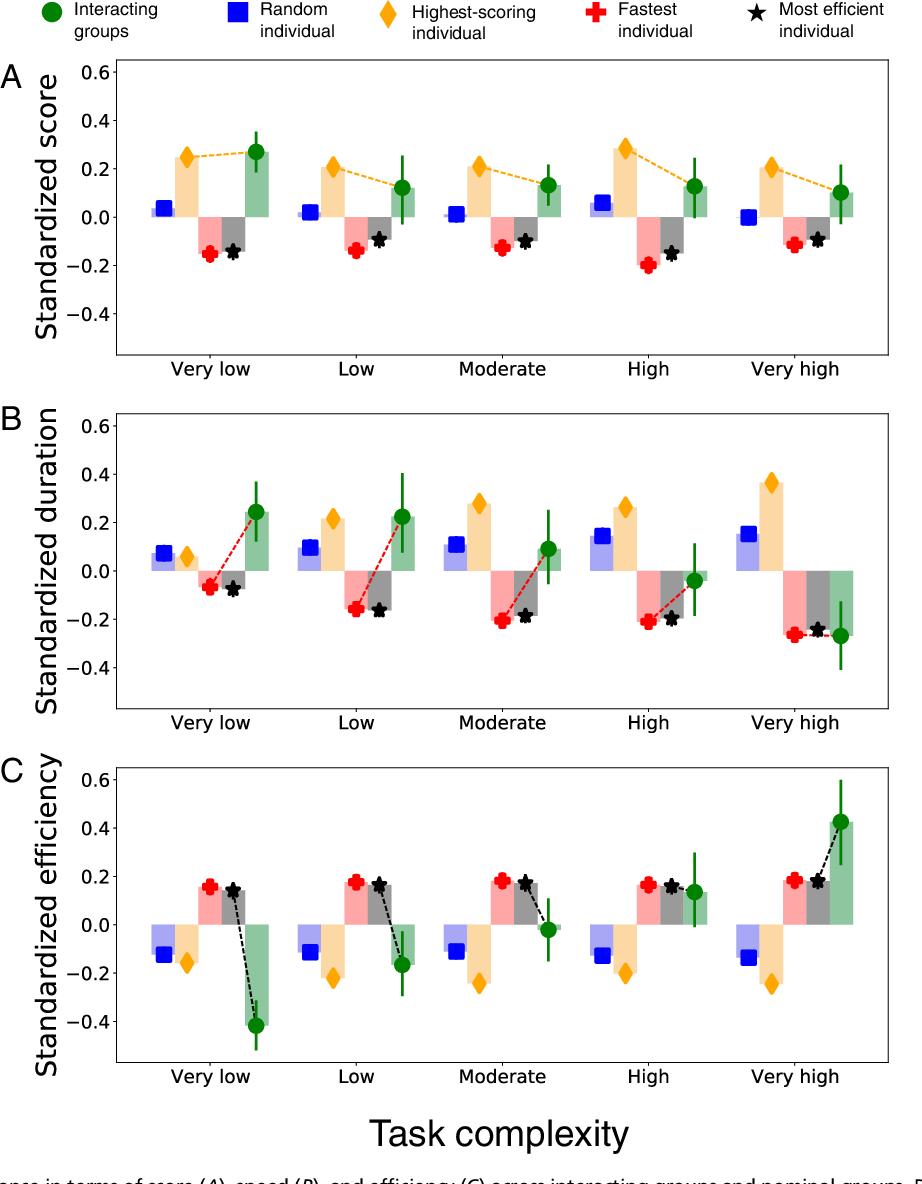
Fig. 3 compara o desempenho geral do grupo padronizado (transformado em pontuações z dentro de cada nível de complexidade da tarefa) com as quatro definições nominais de grupo: indivíduo aleatório, indivíduo com pontuação mais alta, indivíduo mais rápido e indivíduo mais eficiente.
Comparar o desempenho em termos de pontuação (A), velocidade (B) e eficiência (C) entre grupos de interação e grupos nominais. Os dados são combinados em todos os seis blocos e padronizados (ou seja, transformados em pontuações z) dentro de cada nível de complexidade da tarefa (as diferenças são relativas dentro do nível de complexidade e não devem ser comparadas entre os níveis de complexidade). As barras de erro indicam os intervalos de confiança de 95%. Repetimos as análises apresentadas nesta figura para cada bloco, com resultados qualitativamente semelhantes (SI Apêndice, seção S3 e Figs. S8–S10).
Desempenho como qualidade da solução.
Para todos os níveis de complexidade da tarefa, a Fig. 3A mostra que os grupos pontuam mais alto do que os membros selecionados aleatoriamente, mais rápidos e mais eficientes de grupos nominais de tamanho equivalente ( P = 0,013, 95% CI [0,026, 0,225]; P < 0,001, 95% CI [0,184, 0,410]; P < 0,001, 95% CI [0,155, 0,378]; respectivamente), mas inferior à pontuação mais alta membro (P = 0,047, 95% CI [-0,159, -0,001]; consulte o Apêndice SI, Tabelas S4–S7, para tabelas de regressão). Esse resultado é consistente com descobertas de longa data (33⇓⇓⇓–37) de que os grupos interativos geralmente superam os grupos nominais em termos de qualidade da solução quando o padrão é definido por um critério de membro médio (sinergia fraca), mas não quando é definido por um critério de melhor membro (forte sinergia).
Desempenho como velocidade.
Fig. 3B mostra que os grupos de interação concluem tarefas mais complexas - mas não as mais simples - mais rapidamente do que os membros aleatórios e de pontuação mais alta de grupos nominais de tamanho equivalente. Além disso, os grupos de interação são tão rápidos quanto os membros mais rápidos e eficientes na maior complexidade da tarefa (consulte o Apêndice SI, Tabelas S8–S10, para tabelas de regressão). Isso sugere que, de fato, para tarefas com muitos componentes (alunos e salas) e interdependências densas (muitas restrições), os benefícios de distribuir o trabalho para um grupo podem superar as perdas de processo associadas à interação de grupos, o que é consistente com as descobertas em trabalhos anteriores ( 36).
Desempenho como eficiência.
Finalmente, a Fig. 3C mostra que para as tarefas mais complexas os ganhos em velocidade superam os déficits na pontuação. Isso resulta em uma notável interação entre a complexidade da tarefa e o arranjo do trabalho: enquanto os grupos interativos são consideravelmente menos eficientes do que membros selecionados de grupos nominais em tarefas simples, sua eficiência relativa aumenta com a complexidade da tarefa até que superem os de maior pontuação, os mais rápidos e os mais eficientes. membros na complexidade mais alta (consulte o Apêndice SI, Tabelas S11–S13, para tabelas de regressão). Este resultado é uma reminiscência da tomada de decisão em grupo entre insetos sociais, em que um estudo recente descobriu que as colônias de formigas superam as formigas individuais quando a tarefa de discriminação é difícil, mas não quando é fácil (38).
Descompactando a sinergia do grupo.
A descoberta de que os grupos de interação são mais eficientes do que os melhores membros selecionados de grupos nominais de tamanho equivalente - por qualquer uma de nossas quatro definições - quando a tarefa é complexa, mas não quando a tarefa é simples, sugere que o equilíbrio entre perdas de processo e ganhos sinérgicos depende da complexidade da tarefa. Para entender melhor essa dependência, e observando que a variação de eficiência aparente em (Fig. 2C) é mais dependente da variação na duração da tarefa (que varia entre 2 e 6 min em média, Fig. 2B) do que na variação da pontuação alcançada (que varia entre 95% e 85% em média, Fig. 2A), apresentamos a seguir uma análise exploratória do tempo gasto em cada etapa de resolução da tarefa. Essa análise é possível devido à natureza altamente granular de nossos dados. Como cada ação realizada por cada participante é marcada com data e hora, podemos particionar o tempo geral da solução em segmentos medidos com muita precisão que correspondem a estágios distintos do processo de solução de problemas. Para maior clareza, definimos quatro segmentos principais, ilustrados esquematicamente na Fig. 4A:
Marcos de conclusão da tarefa. (A) Os quatro marcos no processo de solução de problemas: (i) a primeira solução intermediária é gerada, (ii) a melhor solução intermediária é gerada, (iii) a solução final é gerada e (iv) a solução final é submetido. (B, D, F e H) O tempo gasto (em minutos) por grupos e indivíduos (seja aleatório, com maior pontuação, mais rápido ou mais eficiente) em cada segmento de tempo. (C, E, G e I) O tempo padronizado gasto (transformado em escores z; ou seja, mostrando a diferença relativa dentro do nível de complexidade) em cada segmento de tempo. As barras de erro indicam os intervalos de confiança de 95%.
Tempo para a primeira solução, .
O tempo desde o início da tarefa até a geração da primeira solução pode ser visto como o tempo gasto na formulação de uma estratégia para abordar a tarefa.
Tempo para a melhor solução, .
A melhor solução não é necessariamente aquela enviada porque a instância da tarefa só termina quando um grupo/indivíduo decide enviar uma solução, e grupos/indivíduos podem gerar soluções após sua melhor solução sem retornar a ela.
Tempo desde a melhor solução até a final, .
O tempo gasto entre a geração da melhor solução e a final, que pode ser visto como "excesso de exploração", diminui a eficiência, pois leva a uma qualidade de solução menor (ou igual), mas maior duração total da tarefa.
Tempo desde a solução final até o envio, .
O tempo gasto entre a geração da solução final e a decisão de enviá-la, que pode ser visto como “ tempo de compromisso” pode ser outra fonte de ineficiência, pois leva a uma qualidade de solução igual, mas aumenta a duração total da tarefa.
Fig. 4 mostra dois conjuntos de comparações entre grupos nominais e interativos para cada um desses quatro segmentos. A Fig. 4 B, D, F e H mostram as durações brutas para , , e
Primeiro, observamos que (em média) os grupos de interação gastam menos tempo em (tempo para a primeira solução, Fig. 4 B e C) do que os membros de grupos nominais, independentemente da complexidade da tarefa ( para todos; e Apêndice SI, Tabela S14). Especulamos que essa observação pode estar relacionada a argumentos de estudos recentes de que a participação em grupos reduz o senso de responsabilidade e o arrependimento que os membros podem enfrentar nas mesmas circunstâncias individualmente. Se correto, uma barreira emocional reduzida à ação pode ser um mecanismo subjacente que leva os membros do grupo a agir mais cedo (39).
Em segundo lugar, observamos um efeito perceptível da complexidade da tarefa em (tempo para a melhor solução, Fig. 4 D e E): os grupos que interagem são mais lentos para alcançar sua melhor solução encontrada do que os mais rápidos e membros mais eficientes de grupos nominais para a tarefa menos complexa, mas mais rápidos para a tarefa mais complexa (P < 0,001, ICs de 95% [0,119, 0,385] e [0,109, 0,371], respectivamente, na complexidade mais baixa e P < ; 0,001, ICs de 95% [−0,351, −0,085] e [−0,370, −0,108], respectivamente, na complexidade mais alta; consulte as Tabelas S17–S18 do Apêndice SI para tabelas de regressão). É importante notar que a maior parte da duração da tarefa é gasta neste segmento, sugerindo que a velocidade para a melhor solução é o principal contribuinte para a sinergia do grupo. Uma possível explicação de por que os grupos de interação são mais rápidos em encontrar a melhor solução em alta complexidade é que os grupos de interação percebem alguns benefícios da divisão de trabalho (consulte o Apêndice SI, seção S4 e Fig. S11, para obter evidências sugestivas). Outra explicação possível, para a qual vemos algumas evidências anedóticas nos logs de bate-papo (SI Apêndice, Fig. S11), é que os grupos de interação estão mais dispostos a satisfazer aceitando uma solução atualmente disponível como satisfatória (40). Ainda outra pode ser que eles se beneficiem da troca de turnos, em que uma pessoa é principalmente ativa, enquanto as outras estão considerando seu(s) próximo(s) movimento(s). Infelizmente, o projeto atual do experimento não nos permite discriminar entre essas explicações alternativas, portanto, elas permanecem especulativas.
Em terceiro lugar, observamos que, independentemente da complexidade, os grupos de interação passam mais tempo no segmento (excesso de exploração, Fig. 4 F e G) em relação aos membros dos grupos nominais; assim como com , a diferença é consistente entre os níveis de complexidade (consulte o Apêndice SI e as Tabelas S19–S20 para tabelas de regressão). Em quarto lugar, os grupos de interação também gastam mais tempo para se comprometer com uma solução () do que os membros selecionados de grupos nominais, mais uma vez independentemente da complexidade (Fig. 4 H e I e Apêndice SI, Tabela S14) . Especulamos que o fato de os grupos em interação poderem se comunicar via chat (e não terem um líder designado) pode adicionar pressão aos grupos para garantir que suas decisões sejam tomadas coletivamente (ou seja, chegar a um consenso), o que poderia contribuir para o efeito observado.
Quinto, observamos que a duração média total da tarefa varia de min em complexidade muito baixa a min em complexidade muito alta (de um máximo de 10 min), o que significa que os participantes geralmente enviam a solução e encerram a instância da tarefa antes de esgotar o tempo. Essa observação é relevante para nossa análise, pois nossas comparações de desempenho de grupos interativos com membros selecionados de grupos nominais não são afetadas pela restrição de tempo.
Resumindo, a Fig. 4 revela dois tipos de perdas de processo (ou seja, o tempo extra gasto em exploração excessiva e obtenção de consenso) e dois tipos de sinergias (ou seja, tempo mais rápido para a primeira solução e tempo mais rápido para a melhor solução para tarefas complexas ). Curiosamente, enquanto as sinergias – especificamente no tempo para a melhor solução – dependem da complexidade da tarefa, as perdas do processo não. Em outras palavras, nossas descobertas sugerem que estar em um grupo interativo tem custos fixos que são relativamente consistentes entre os níveis de complexidade da tarefa, mas um benefício que varia entre os níveis de complexidade (ou seja, menos tempo gasto para encontrar a melhor solução).
Para esclarecer ainda mais essa descoberta, agregamos os custos e benefícios para quantificar o valor da execução da tarefa em um grupo de interação em níveis de complexidade. Em particular, medimos cada custo e benefício como a diferença absoluta, em termos de tempo gasto, entre grupos de interação e membros aleatórios (ou seja, médios) de grupos nominais em cada segmento de tempo:
Fig. 5 mostra que o custo total associado às ineficiências do grupo de interação (ou seja, excesso de exploração, obtenção de consenso) excede os benefícios sinérgicos (ou seja, ganhos de velocidade para encontrar a melhor solução) ao resolver tarefas de baixa complexidade, mas não de alta complexidade. Isso explica nossa descoberta de que os grupos são mais eficientes do que os membros com maior pontuação, mais rápidos e mais eficientes de grupos nominais de tamanho equivalente quando a tarefa é complexa, mas essa relação é invertida quando a tarefa é simples. Encontramos resultados semelhantes para a comparação de membros com pontuação mais alta (SI Apêndice, seção S5 e Fig. S12).
O custo-benefício dos grupos interativos. A figura ilustra a diferença absoluta em termos de tempo médio gasto entre grupos de interação e um grupo nominal individual médio em cada segmento de tempo.
Explorando as diferenças nas abordagens de resolução de problemas.
Recapitulando nossos principais resultados, os grupos interativos são mais eficientes até mesmo do que o membro mais eficiente de grupos nominais para problemas de alta complexidade; portanto, concluímos que eles exibem forte sinergia para eficiência (Fig. 3C). Em relação à velocidade, os grupos de interação são mais rápidos do que o membro médio (escolhido aleatoriamente) e tão rápido quanto o membro mais rápido de grupos nominais de tamanho equivalente (Fig. 3B), exibindo assim apenas uma sinergia fraca. Para a qualidade da solução, os grupos interativos exibem sinergia ainda mais fraca, pois pontuam mais alto do que o membro médio, mas não tão bem quanto o membro com pontuação mais alta dos grupos nominais (Fig. 3A).
Para investigar melhor esses resultados, examinamos o número e o ritmo das soluções intermediárias geradas, onde uma solução intermediária é definida como uma atribuição de alunos a salas (ou seja, cada ação realizada por um participante gera uma solução intermediária). Conforme mostrado nas Figuras 6 A e B, observamos que os grupos não apenas geraram mais soluções intermediárias do que os membros aleatórios, com maior pontuação, mais rápidos e mais eficientes de grupos nominais de tamanho equivalente ( para todos, ICs de 95% , , e respectivamente, Apêndice SI, Tabela S23); eles também o fizeram em uma taxa mais alta ( para todos, ICs de 95% , , e , respectivamente; Apêndice SI, Tabela S23). Os grupos interativos também exibiram um raio de solução mais amplo, definido como a distância máxima de edição (ou seja, o número de diferenças nas atribuições de alunos/salas) entre a primeira solução completa (ou seja, todos os alunos atribuídos a salas, mas os conflitos podem não ser resolvidos) e todas as subseqüentes soluções completas, sugerindo que eles exploraram o espaço de soluções de forma mais ampla (Fig. 6C; para todos, ICs de 95% , , e respectivamente; Apêndice SI, Tabela S23). Também confirmamos esta conclusão qualitativa usando duas outras medidas de exploração: a porcentagem de soluções dentro de uma distância de edição de dois da solução final e a porcentagem de soluções intermediárias que envolveram uma violação de restrição (SI Apêndice, Figs. S13 e S14).
Diferenças mecanísticas nas abordagens de resolução de problemas entre grupos e indivíduos em interação. Grupos interativos geram (A) mais soluções, (B) em um ritmo mais rápido e (C) exploram o espaço de soluções de forma mais ampla. (D) No entanto, a qualidade da melhor solução encontrada (submetida ou não) não é melhor do que a solução encontrada pelos grupos nominais individuais de maior pontuação. As barras de erro indicam os intervalos de confiança de 95%.
À luz dessas observações, é ainda mais surpreendente que os grupos de interação não tenham encontrado soluções de maior qualidade do que o membro de maior pontuação dos grupos nominais (Fig. 6D; ; Apêndice SI, Tabela S23). Em parte, a lacuna pode ser explicada pela interação dos grupos que também falham em enviar sua solução mais encontrada em uma taxa mais alta do que o indivíduo com pontuação mais alta: em todas as complexidades, o indivíduo com pontuação mais alta falha em enviar sua solução mais encontrada das vezes, enquanto os grupos de interação falham em apresentar suas melhores soluções das vezes (; diferença nas proporções). Como resultado, as soluções apresentadas pelos grupos interativos foram piores em relação aos membros individuais com pontuação mais alta do que se todos tivessem apresentado sua melhor solução encontrada (compare a Fig. 3A com a Fig. 6D), embora mesmo assim alguma lacuna permaneça.
O que pode explicar a combinação de forte sinergia em eficiência e apenas fraca sinergia para qualidade e velocidade da solução? Pesquisas anteriores que conceituam a solução de problemas como uma busca adaptativa em uma paisagem de desempenho acidentada (14, 27), em que cada ponto na paisagem representa uma solução para a atribuição da sala e a altura do ponto representa o desempenho dessa atribuição, fornece vários, explicações possivelmente inter-relacionadas. Uma possível explicação é que os indivíduos com pontuação mais alta têm melhores representações (aproximações de menor dimensão) do verdadeiro cenário de desempenho, o que lhes permite avaliar soluções (e trajetórias de solução) offline sem testá-las por meio de experimentação (41, 42). Melhores representações podem levar a avaliações off-line mais precisas e esforços de busca mais eficazes (26, 43, 44), caracterizados por menos soluções intermediárias e maior qualidade de solução. Alternativamente, grupos de solucionadores de problemas podem ter interesses conflitantes (por exemplo, maximizar a pontuação versus minimizar a duração) e, portanto, visões diferentes do curso de ação correto (45). Se for verdade, os grupos podem se beneficiar da coordenação central, designando um líder de grupo (45) ou de intervenções relacionadas ao processo, como impor interrupções intermitentes na interação (46, 47). Ainda outra possibilidade é que, quando o tempo é limitado, as estratégias de busca que permitem ganhos rápidos (ou seja, grandes melhorias de desempenho desde o início) e reduzem a quantidade de exploração podem parecer superiores (26). Portanto, embora a estratégia de busca local de aprofundamento do caminho (por exemplo, subida de colina) adotada pelos membros com pontuação mais alta de grupos nominais de tamanho equivalente possa fornecer benefícios de desempenho de curto prazo, a estratégia dos grupos de interação de ampliar o domínio de pesquisa pode ser mais vantajosa a longo prazo (48, 49).
Discussão
Para muitas tarefas de interesse, os gerentes podem decidir se atribuem uma tarefa a um grupo interativo ou a um número comparável de indivíduos trabalhando independentemente (12). Para configurações como essas, nossos resultados oferecem vários insights. Primeiro, as decisões sobre como alocar o trabalho – para grupos de interação ou para grupos nominais – devem depender da complexidade da tarefa em questão e da forma como o desempenho é avaliado. Por exemplo, se um gerente quiser encontrar uma solução viável para um CSOP no menor tempo possível, a recomendação seria pedir a um grupo para resolver o problema quando o problema for complexo, mas pedir a solucionadores de problemas independentes quando for simples. Vale ressaltar que os resultados de duração e eficiência apresentados aqui podem, na verdade, subestimar como isso funcionaria na prática. Por exemplo, se o trabalho fosse organizado em grupos nominais, esse arranjo ainda produziria várias soluções diferentes para algum gerente decidir entre elas. Embora nossa operacionalização de grupos nominais simule uma situação em que o gerente toma a decisão instantaneamente, há circunstâncias em que um gerente pode querer considerar os méritos das diferentes soluções, e isso levaria um tempo diferente de zero. Não é o caso dos grupos de interação, onde o processo de decisão já está incluído no tempo decorrido do exercício de resolução de problemas.
Em segundo lugar, nossas descobertas também sugerem que uma possível explicação de por que as perdas de processo de grupo figuram com mais destaque nas descobertas de pesquisa do que os ganhos sinérgicos (12) é que os estudos de laboratório de desempenho de grupo geralmente dependem de tarefas muito simples. De fato, a evidência laboratorial mais clara até hoje para um desempenho de grupo superior, embora rara, vem de grupos que trabalham em tarefas relativamente complexas (13, 46, 50, 51); no entanto, o fato de que a complexidade da tarefa não variou sistematicamente em um único estudo representa uma importante fonte de variação descontrolada em pesquisas anteriores (17, 36).
Em terceiro lugar, nossa análise de como grupos de interação e indivíduos independentes diferem no tempo que gastam durante várias partes do processo de resolução de problemas oferece uma visão de como os processos de grupo podem ser melhorados. Por exemplo, nossa descoberta de que os grupos gastam mais tempo decidindo que uma tarefa foi concluída (ou seja, obtendo consenso) sugere que designar um líder de grupo com a capacidade de tomar essa decisão unilateralmente, como um indivíduo, deve reduzir essa fonte de atraso , melhorando assim o desempenho do grupo. Além disso, nossa descoberta de que os grupos de interação têm menos probabilidade de enviar suas melhores soluções encontradas sugere que armazenar suas melhores soluções para que possam ser recarregadas e potencialmente modificadas em etapas subsequentes (um recurso onipresente de software de produtividade pessoal) também deve melhorar seu desempenho ( 46).
Quarto, nossa análise da dinâmica de solução de grupos versus indivíduos provoca quebra-cabeças adicionais para trabalhos futuros. Em particular, se os grupos geram mais soluções com mais rapidez e eficiência em uma faixa mais ampla do espaço de soluções do que os indivíduos com pontuação mais alta, por que eles não encontram soluções melhores?
Finalmente, concluímos que a ciência do desempenho do grupo se beneficiaria de uma apreciação mais profunda e sistemática das semelhanças e diferenças entre as tarefas que os grupos são solicitados a realizar, tanto no laboratório quanto no campo. Há uma necessidade de uma teoria abrangente e empiricamente fundamentada de tarefas de grupo (12). Um programa de pesquisa que variasse sistematicamente os tipos de tarefas, juntamente com os processos de grupo permitidos e outros fatores contextuais, avançaria a ciência básica da solução de problemas em grupo, ao mesmo tempo em que abordaria aplicações práticas.
Materiais e métodos
O estudo foi revisado pelo Microsoft Research Ethics Advisory Board e aprovado pelo Microsoft Research Institutional Review Board (MSR IRB; Aprovação 0000019). Todos os participantes forneceram consentimento explícito para participar deste estudo, e o MSR IRB aprovou o procedimento de consentimento. Nosso projeto experimental, tamanho da amostra e análises comparando o desempenho entre grupos de interação e grupos nominais foram pré-registrados antes da coleta dos dados (AsPredicted 13123). Todas as outras análises são exploratórias.
Algorithmic Solver.
Modelamos cada problema de atribuição de sala como um problema de programação inteira mista e geramos o tempo de execução para os computadores resolverem cada problema usando o software IBM ILOG CPLEX Optimization Studio, que é um solucionador de programação matemática de alto desempenho para programação linear, programação inteira mista e programação quadrática. O software foi executado em um laptop com um microprocessador Intel Core i5 operando a uma velocidade de 2,6 GHz. Executamos o software usando a configuração padrão de parâmetros. A unidade do tempo de execução no arquivo de tarefa é "ticks", que é a unidade do CPLEX para medir a quantidade de trabalho realizado. A correspondência dos tiques com o tempo do relógio varia entre as plataformas (incluindo hardware, software, carga da máquina, etc.), mas dado um problema de programação inteira mista e as configurações de parâmetros, os tiques necessários para resolver um problema são determinísticos. Nesse sentido, a confiabilidade teste-reteste do solucionador algorítmico é 1. Veja o Apêndice SI, seção 1.4.2, para detalhes adicionais.
Análise estatística.
Como cada grupo de interação (ou indivíduo) concluiu as cinco tarefas de atribuição de sala, realizamos testes para diferenças entre as condições no nível da tarefa. Para efeitos de interação, modelamos os dados usando um modelo misto linear generalizado para cada resultado (por exemplo, pontuação, duração e eficiência) com um efeito aleatório para o grupo ou identificador individual. Esses modelos respondem pela estrutura aninhada dos dados. Todos os testes estatísticos foram bicaudais (conforme nosso pré-registro). Os detalhes dos testes estatísticos estão no Apêndice SI, seção S7.
Coeficientes padronizados.
Para permitir comparações significativas de tamanhos de efeito em tarefas de diferentes níveis de complexidade, padronizamos várias métricas de desempenho (por exemplo, pontuação, duração, eficiência e número de soluções) dentro de cada nível de complexidade. Por exemplo, o valor padronizado da medida X, medido para a instância de tarefa i de complexidade c, é definido comoonde
Disponibilidade de dados
Dados e códigos de replicação estão disponíveis no Harvard Dataverse, https://doi.org/10.7910/DVN/RP2OCY (52). O experimento foi desenvolvido na plataforma Empirica (53). O código-fonte da tarefa de atribuição de sala pode ser encontrado em https://github.com/amaatouq/room-assignment-csop, e o código-fonte do teste Reading the Mind in the Eyes pode ser encontrado em https://github .com/amaatouq/rme-test.
Agradecimentos
Agradecemos a Valery Yakubovich, Hazhir Rahmandad e James Houghton por suas discussões e comentários úteis. Os autores agradecem à Fundação Alfred P. Sloan (G-2020-13924) pelo apoio financeiro.
Notas de rodapé
Contribuições dos autores: A.A., M.Y. e D.J.W. pesquisa planejada; A.A., M.Y. e D.J.W. pesquisas realizadas; A.A., M.A., M.Y. e D.J.W. contribuiu com novos reagentes/ferramentas analíticas; A.A., M.A., M.Y. e D.J.W. dados analisados; e A.A., M.A., M.Y. e D.J.W. escreveu o papel.
Os autores declaram não haver interesses concorrentes.
Este artigo é uma submissão direta do PNAS.
Este artigo contém informações de suporte on-line em https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2101062118/-/DCSupplemental.
Este artigo de acesso aberto é distribuído sob licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 (CC BY-NC-ND).




