Nous avons demandé au cosmologue Pau Figueras tout ce que vous avez toujours voulu savoir sur les trous noirs. Dans l'autre partie de l'interview, il a expliqué ce que sont les trous noirs, physiquement, et comment nous espérons les observer. Dans cette seconde partie de l'entretien, il explique comment les théories d'Einstein prédisent leur existence, et comment les décrire mathématiquement.
Veuillez noter que depuis que cette interview a été menée, des preuves tangibles de trous noirs ont été détectées. Il vient des ondes gravitationnelles. Voir Les trous noirs existent ! pour en savoir plus.
Comment les trous noirs ont-ils été prédits pour la première fois ?
Einstein a publié sa [théorie générale de la relativité] à la fin de 1915,
et seulement quelques mois plus tard, au début de 1916, [Karl]
Schwarzschild a trouvé la première solution des équations d'Einstein. [Par solution, nous entendons certaines valeurs des variables décrivant la courbure de l'espace-temps et la distribution de la matière qui satisfont aux équations d'Einstein.]
[Cette solution] décrit le champ gravitationnel d'un corps à symétrie sphérique : un trou noir.
A l'époque, il n'était pas compris que cette solution correspondait à une
trou noir. En fait, même dans les années 30, les plus grands esprits de l'époque,
[y compris] Einstein lui-même, méprisait l'idée d'un trou noir
car il contenait une singularité, à savoir un lieu où la courbure est
si grand que même la relativité générale s'effondre. Il a fallu près de 50
années pour vraiment comprendre ce qu'est un trou noir, et cela n'a été fait que dans les années 1960.
La relativité générale affirme que les objets massifs courbent l'espace-temps. Comment les trous noirs affectent-ils la courbure de l'espace-temps ?
La force du champ gravitationnel est mesurée en termes de courbure. Et parce que les trous noirs sont très massifs et très petits, leur gravité est très forte et [crée] une très grande courbure de l'espace-temps.
Une façon de caractériser la courbure est ce qu'on appelle le rayon de Schwarzschild :
où $G_ N$ est la constante [de gravité] de Newton, $M$ est la masse de l'objet et $c$ est la vitesse de la lumière.
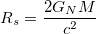
Le rayon de Schwarzschild est, plus ou moins, la taille qu'un objet donné, avec une masse donnée, devrait avoir pour qu'il soit un trou noir. Par exemple, si nous parvenions à concentrer toute la masse de la Terre dans une sphère d'un rayon de quelques centimètres, alors cet objet serait un trou noir.
Bien sûr, nous savons que cela ne peut pas arriver parce qu'il y a d'autres forces dans la nature qui l'empêchent, mais dans d'autres circonstances, cela peut arriver. Par exemple, lorsque des étoiles très massives manquent de combustible nucléaire, elles se refroidissent et s'effondrent, et à un moment donné elles deviennent suffisamment petites pour que toute la masse s'insère dans un rayon de Schwarzschild – elles forment donc un trou noir.
Par exemple, le rayon de Schwarzschild du Soleil est de l'ordre de quelques kilomètres. Donc si on parvenait à concentrer toute la masse du Soleil dans une sphère de quelques kilomètres, alors ce serait un trou noir.
ound:white">
Pouvez-vous caractériser un trou noir si simplement, avec seulement quelques caractéristiques, telles que la masse et la taille ?
L'une des raisons pour lesquelles les trous noirs sont si importants dans notre compréhension de la relativité générale est leur simplicité , car ils sont constitués des éléments constitutifs les plus fondamentaux de la théorie, à savoir l'espace et le temps seuls. Ils sont très simples et donc nous pouvons les comprendre.
Ceci [est en contraste avec] d'autres objets gravitationnels, tels que les étoiles. Afin de comprendre une étoile, [en plus d'avoir besoin] de prendre en compte la relativité générale, vous devez également comprendre la physique nucléaire pour prendre en compte les réactions nucléaires [et] la physique des plasmas pour comprendre le transport de la chaleur au sein de l'étoile. Cela devient très compliqué et nous sommes souvent amenés à étudier ces objets dans certaines approximations.
Nous n'avons pas à faire cela avec les trous noirs car ils ne sont constitués que d'espace et de temps, nous en avons donc une compréhension complète au sein de notre seule théorie. Nous n'avons besoin d'aucune autre physique. Cette simplicité se traduit par le fait qu'ils sont simplement décrits en termes de très peu de paramètres.
Dans le cas du vide, si le trou noir est statique, alors il doit être sphérique et il n'y a qu'un seul paramètre caractérisant le trou noir, à savoir sa masse. [Cependant], les objets dans la nature, comme les étoiles, tournent, donc les trous noirs qui se produisent dans la nature devraient avoir une certaine rotation. La solution de Schwarzschild a été trouvée [juste] quelques mois après qu'Einstein a publié sa théorie, mais il a fallu 50 ans de plus pour trouver la solution générale qui a une rotation et qui est pertinente pour décrire les trous noirs [que nous pourrions trouver dans] la nature. Cette solution de Kerr est entièrement décrite par seulement deux paramètres, à savoir la masse et le spin du trou noir. Avec ces deux paramètres, vous pouvez caractériser complètement tous les trous noirs dans la nature et nous n'avons pas besoin de faire d'approximations pour comprendre ces objets. C'est pourquoi ils sont si importants.
Dans un sens, les trous noirs ne sont pas différents des particules élémentaires [en physique des particules] car nous n'avons besoin de spécifier que quelques paramètres [pour les décrire]. La même chose avec les trous noirs - [ils] sont les particules élémentaires de la relativité générale.
Les trous noirs sont-ils le plus grand mystère ouvert de la relativité générale ?
Oui. Les trous noirs sont une prédiction de la relativité générale et nous connaissons plusieurs cas dans la nature où nous pensons qu'ils devraient se produire, mais nous ne les avons pas encore détectés. C'est donc toujours une question ouverte de savoir s'ils [existent] ou non, ou s'ils ont les propriétés que la relativité générale prédit.
Ceci est important car la plupart des tests [de] la relativité générale [impliquent] des situations où la gravité est faible, ou relativement faible. Par exemple, nous avons testé la courbure de la lumière, la précession du périhélie de Mercure.
La détection des trous noirs serait importante parce que les signaux que nous
obtiendraient, à savoir ces ondes gravitationnelles, seraient générées dans
régions où la gravité est très forte. Cela nous permettrait de tester le régime de champ fort de la relativité générale, ce que nous n'avons pas pu faire jusqu'à présent. Cela mettrait des tests très forts sur la relativité générale, il est donc très important que nous [observions] les trous noirs : [les observations nous donneraient] une toute nouvelle fenêtre sur la relativité générale.




