Importance
Les scientifiques et les gestionnaires se sont préoccupés de savoir si et, le cas échéant, dans quelles conditions, les groupes de résolveurs de problèmes en interaction surpassent les individus autonomes. Nous décrivons ici une expérience dans laquelle des individus et des groupes ont été évalués sur une série de tâches de complexité variable. Nous constatons que les groupes sont aussi rapides que l'individu le plus rapide et plus efficaces que l'individu le plus efficace lorsque la tâche est complexe mais pas lorsque la tâche est simple. Nous quantifions ensuite avec précision les gains synergiques et les pertes de processus associés aux groupes en interaction, constatant que l'équilibre entre les deux dépend de la complexité. Notre étude a le potentiel de concilier des résultats contradictoires sur la synergie de groupe dans des travaux antérieurs.
Résumé
La complexité, définie en termes de nombre de composants et de la nature des interdépendances entre eux, est clairement une caractéristique pertinente de toutes les tâches exécutées par les groupes. Pourtant, le rôle que joue la complexité des tâches dans la détermination de la performance du groupe reste mal compris, en partie parce qu'il n'existe pas de langage clair pour exprimer la complexité d'une manière qui permette des comparaisons directes entre les tâches. Ici, nous évitons cette difficulté analytique en identifiant une classe de tâches pour lesquelles la complexité peut varier systématiquement tout en gardant inchangés tous les autres éléments de la tâche. Nous testons ensuite les effets de la complexité des tâches dans une expérience préenregistrée en deux phases dans laquelle 1 200 individus ont été évalués sur une série de tâches de complexité variable (phase 1) puis assignés au hasard pour résoudre des tâches similaires soit dans des groupes en interaction, soit en tant qu'individus indépendants ( phase 2). Nous constatons que les groupes en interaction sont aussi rapides que l'individu le plus rapide et plus efficaces que l'individu le plus efficace pour les tâches complexes mais pas pour les plus simples. En exploitant nos données numériques hautement granulaires, nous définissons et mesurons précisément les pertes de processus de groupe et les gains synergiques et montrons que l'équilibre entre les deux commutateurs se situe à des valeurs intermédiaires de la complexité des tâches. Enfin, nous constatons que les groupes en interaction génèrent plus de solutions plus rapidement et explorent l'espace des solutions plus largement que les résolveurs de problèmes indépendants, trouvant des solutions de meilleure qualité que tous les individus sauf les plus performants.
Les tâches effectuées par des groupes de résolveurs de problèmes en interaction, que ce soit dans le monde réel ou dans des contextes expérimentaux, varient selon un certain nombre de dimensions qui influencent de manière plausible la performance du groupe (1⇓⇓⇓⇓–6). Dans cet article, nous nous concentrons sur une dimension importante mais empiriquement sous-étudiée des tâches, la complexité, qui est généralement comprise comme dépendant d'au moins deux facteurs : (i) le nombre de composants distincts qui constituent une tâche et (ii) le nombre, la force , et configuration des interdépendances entre ces composants (7⇓⇓⇓–11).
Intuitivement, la complexité des tâches est d'une importance évidente pour les performances du groupe. Toutes choses égales par ailleurs, on s'attendrait à ce que les résolveurs de problèmes obtiennent de moins bons résultats sur des tâches qui ont plus de composants ou pour lesquelles les interactions entre les composants sont plus denses. En outre, on pourrait également s'attendre à ce que la complexité des tâches ait un impact sur la «synergie» du groupe, définie comme une performance supérieure à ce qui serait attendu d'un groupe de taille similaire d'individus travaillant de manière indépendante, c'est-à-dire un «groupe nominal» (12). Dans ce cas, cependant, il est moins évident de savoir quelle serait la direction de l'effet. D'une part, les groupes en interaction peuvent être plus performants que les groupes nominaux sur des tâches complexes, car ils sont capables de répartir les efforts (13), de partager des informations sur des solutions de haute qualité (14) ou de corriger des erreurs (15). D'un autre côté, avec des tâches plus complexes, les groupes en interaction peuvent subir des pertes de processus encore plus importantes - y compris le relâchement social (16), la pensée de groupe (17) et les conflits interpersonnels (4) - peut-être parce que les tâches complexes imposent de plus grandes exigences aux contributeurs individuels et offrent plus d'opportunités de rester coincé dans des optima locaux globalement sous-optimaux, l'un ou l'autre pouvant également entraîner une augmentation du stress et une sous-performance par rapport aux groupes nominaux.
Un défi majeur pour résoudre les questions sur les effets de la complexité des tâches est que, bien que le concept de haut niveau semble intuitif, il n'a pas encore été suffisamment opérationnalisé pour permettre aux chercheurs de quantifier la complexité des différents types de tâches et donc de faire des pommes aux pommes comparaisons entre eux. Au contraire, les opérationnalisations existantes sont souvent elles-mêmes complexes. Par exemple, un modèle répertorie 27 facteurs contribuant à la complexité regroupés sous 10 dimensions de complexité (9), tandis que d'autres modèles sont suffisamment spécifiques à un domaine pour que les différences numériques entre différents types de tâches soient difficiles à interpréter (7). Ajoutant à la confusion, certaines définitions mettent l'accent sur la complexité objective, se référant uniquement aux caractéristiques de la tâche qui peuvent être mesurées indépendamment de ceux qui exécutent une tâche, tandis que d'autres mettent l'accent sur la complexité subjective, la complexité de la tâche telle qu'elle est vécue par ceux qui l'exécutent (9, 11).
Ici, nous évitons ces difficultés analytiques en identifiant une classe de tâches pour lesquelles la complexité peut varier systématiquement tout en gardant fixes tous les autres éléments de la tâche. De cette manière, nous pouvons facilement mesurer les performances en fonction de la complexité croissante sans nous soucier des confusions résultant d'autres aspects de la tâche tels que le type de tâche (3) ou d'autres caractéristiques des processus de groupe (4, 18). En outre, nous exigeons que nos tâches puissent être exécutées de manière réaliste soit de manière indépendante, soit en collaboration, permettant ainsi une comparaison directe entre les groupes nominaux et les groupes en interaction.
Une classe de tâches qui satisfont à ces critères sont les problèmes de satisfaction de contraintes et d'optimisation (CSOP), qui sont largement étudiés en intelligence artificielle et en recherche opérationnelle. Le lien avec la recherche opérationnelle est utile car, contrairement à d'autres problèmes «jouets», les CSOP correspondent de manière relativement intuitive à une gamme de problèmes pratiques d'allocation des ressources et ont été utilisés pour modéliser de nombreux problèmes d'intérêt pratique. Des exemples de CSOP incluent des projets de logiciel de dotation où il y a plusieurs affectations potentielles de développeur à activité à évaluer (19) ; former des groupes d'apprentissage en fonction de certains critères liés aux objectifs de collaboration (20); horaires ferroviaires (21); et allouer des vaccins, des ventilateurs et des fournitures médicales pendant la pandémie de COVID-19 (22). De plus, bien que les CSOP capturent des caractéristiques importantes des exercices de résolution de problèmes en groupe dans le monde réel, ils n'exigent pas que les participants aient des compétences spécialisées. En conséquence, les participants peuvent être recrutés à partir de services en ligne, ce qui réduit le coût et la difficulté de coordonner la participation simultanée des groupes. Enfin, comme pour d'autres problèmes complexes (14, 23⇓–25), la fonction de gain pour les CSOP peut être décrite comme un paysage de performance robuste, où chaque point du paysage représente une combinaison de choix potentiellement interdépendants (une solution au problème) , tandis que la hauteur du point représente la performance de cette combinaison (26, 27). Par conséquent, les CSOP peuvent être caractérisés par plusieurs solutions localement optimales mais globalement sous-optimales (26, 27) et se prêtent donc potentiellement à de nombreuses stratégies et styles de solutions, sans stratégie unique universellement supérieure (28).
Le CSOP spécifique que nous avons étudié est un problème d'attribution de salle dans lequel les participants, individuellement ou en groupe, attribuent N étudiants à M salles où chaque étudiant a une utilité spécifiée pour chaque salle (Annexe SI, section 1.1). L'objectif de la tâche est de maximiser l'utilité totale de l'élève tout en respectant les contraintes Q (par exemple, "Les élèves A et J ne peuvent pas partager une chambre ou être dans des chambres adjacentes"). Lorsque la tâche est effectuée en groupe, les participants sont autorisés à communiquer via un chat textuel et à déplacer simultanément différents étudiants, effectuant ainsi un traitement parallèle s'ils le souhaitent. Essentiellement pour nos besoins, la complexité de la tâche peut varier systématiquement en ajustant seulement trois paramètres clés : le nombre d'étudiants , le nombre de salles et le nombre de contraintes . En effet, un avantage significatif de cette tâche (et des CSOP en général) par rapport aux tâches plus couramment étudiées dans les paramètres de performance de groupe est que sa complexité peut être quantifiée en termes de temps d'exécution requis par un solveur algorithmique pour trouver la solution optimale, permettant nous permet de classer facilement les instances de tâches par complexité (voir Matériels et méthodes pour plus de détails). La figure 1 illustre comment la complexité peut varier entre deux instances du problème d'attribution de salle. Dans un cas de faible complexité, six étudiants doivent être affectés à quatre chambres soumises à seulement deux contraintes ("B et E doivent être voisins" et "C et F ne peuvent pas vivre dans la même chambre"). Dans une instance à haute complexité, 18 étudiants doivent être affectés à 8 salles soumises à 18 contraintes.
Illustration de la tâche d'attribution de salle. La tâche consistait à affecter N étudiants à M salles afin de maximiser l'utilité totale des étudiants, qui ont chacun une utilité spécifiée pour chaque salle, tout en respectant Q contraintes. La complexité de la tâche est caractérisée par le nombre d'étudiants à affecter , le nombre de dortoirs disponibles et le nombre de contraintes . (Haut) Un cas peu complexe dans lequel six étudiants doivent être affectés à quatre chambres sous réserve de deux contraintes. (En bas) Un cas très complexe dans lequel 18 étudiants doivent être répartis dans 8 salles soumises à 18 contraintes. Voir l'annexe SI, section S1.1, pour plus de détails et l'annexe SI, fig. S1–S2, pour les captures d'écran de l'interface de tâche.
Conception d'expériences
Dans cet article, nous testons l'hypothèse selon laquelle la complexité des tâches modère la performance relative de la résolution de problèmes en groupe par rapport à celle individuelle. À cette fin, nous abordons la question suivante : comment l'équilibre entre les pertes de processus et les gains synergiques dans les groupes en interaction dépend-il de la complexité de la tâche ?
Notre expérience s'est déroulée en deux phases. Au cours de la phase 1, 1 200 participants ont effectué individuellement cinq tâches d'affectation de salle : trois tâches de complexité très faible et deux de complexité modérée (annexe SI, tableau S1) ainsi qu'un test standard de lecture de l'esprit dans les yeux (annexe SI, section S1.2 et Fig. S3), qui est couramment utilisé comme mesure de la perception sociale et a été utilisé par plusieurs études récentes reliant la perception sociale à la performance de groupe (18, 29⇓⇓–32).
Après l'achèvement de la phase 1, nous avons noté tous les participants sur le niveau de compétence et la perspicacité sociale afin de pouvoir les affecter à des blocs expérimentaux dans la phase 2 (Annexe SI, section 1.4 et Fig. S4). En tenant compte de ces caractéristiques dans notre procédure de randomisation par blocs de la phase 2, nous avons pu nous assurer que les différents niveaux de compétence et de perception sociale (et leurs combinaisons) étaient équilibrés dans les arrangements de travail de groupe et individuels. L'objectif principal du schéma de randomisation par blocs était de suréchantillonner des combinaisons statistiquement moins fréquentes (par exemple, tous les membres du groupe ayant des compétences élevées ou une perspicacité sociale élevée), augmentant ainsi la puissance statistique de nos expériences. Nous notons que nous nous concentrons ici sur la comparaison entre les groupes en interaction et les groupes nominaux, et non sur les différences de composition entre les groupes en interaction ; ainsi, notre analyse des effets du niveau de compétence et de la perception sociale sur la performance sera publiée ailleurs (selon notre préinscription).
Les mêmes 1 200 participants ont été invités à participer à la phase 2, et les 828 premiers participants qui se sont présentés et ont réussi les contrôles d'attention (conformément à notre préinscription ; voir l'annexe SI, tableau S2, pour la taille des échantillons) ont été affectés à un deuxième séquence de cinq tâches d'attribution de chambre (la séquence de tâches a été randomisée), également de complexité variable (très faible, faible, modérée, élevée et très élevée ; Annexe SI, Tableau S3 et Fig. S5). Toutes les tâches ont expiré à 10 min dans la phase 2, quelle que soit leur complexité. Sur la base des compétences et de la perspicacité sociale de chaque participant, telles que mesurées lors de la phase 1, nous avons d'abord réparti chaque individu en blocs (par exemple, compétences élevées, perspicacité sociale élevée, compétences mixtes, perspicacité sociale élevée, etc.). Ensuite, dans chaque bloc, les participants ont été randomisés dans l'une des deux conditions : une condition de groupe interactif ( participants, formant 197 groupes de taille 3 ; les données pour 1 groupe sont incomplètes, ce qui conduit au nombre de groupes d'interaction valides étant de 196), dans lequel les membres du groupe ont résolu le problème collectivement et pouvaient communiquer entre eux via un chat textuel ; et une condition individuelle indépendante ( participants ; les données de 3 personnes sont incomplètes, ce qui porte le nombre d'individus indépendants valides à 234), dans laquelle chaque participant a travaillé seul sur la tâche qui lui avait été assignée. Tous les résultats présentés ici proviennent de la phase 2 de l'expérience.
Évaluation des performances.
Dans la phase 2, nous avons utilisé trois métriques pour capturer les performances d'une instance de tâche d'attribution de salle : (1) le score normalisé, défini comme le score réel obtenu dans une instance de tâche divisé par le score maximum possible pour cette tâche ; (2) durée (ou temps d'exécution), définie comme le temps écoulé entre le début de la tâche et la soumission d'une solution (ou jusqu'à ce que la tâche expire à 10 minutes) ; et enfin, (3) l'efficacité, définie comme le score normalisé divisé par la durée.
Les trois mesures sont des indicateurs naturels de performance que l'on peut souhaiter optimiser dans certaines circonstances. En l'absence de contraintes de temps, par exemple, le score normalisé est une mesure évidente de la qualité de la solution. En revanche, la durée est appropriée lorsque le temps de résolution des problèmes est plus important que la qualité (par exemple, proposer rapidement un plan raisonnablement bon pour l'allocation des ressources lors d'une intervention en cas de catastrophe), et l'efficacité est appropriée lorsque la qualité et la rapidité sont importantes (par exemple. , dans le développement de produits).
Suite à des travaux antérieurs (12, 33⇓⇓⇓–37), nous évaluons les performances des groupes par rapport à des groupes dits nominaux, définis comme un ensemble d'individus autonomes de même taille. Les groupes nominaux fournissent une référence utile pour les groupes en interaction car ils tiennent compte de la disponibilité différentielle des ressources entre les groupes et les individus (12) ; c'est-à-dire qu'ils s'ajustent à la quantité de ressources intellectuelles que les groupes pourraient apporter (c'est-à-dire les heures de travail) et à la probabilité mathématique qu'au moins un membre ait pu atteindre la même performance. Ainsi, la performance d'un groupe en interaction au-delà de celle d'un groupe nominal peut être attribuée à l'interaction du groupe, et non à des ressources plus importantes.
En général, les comparaisons entre les groupes en interaction et les groupes nominaux de taille équivalente ont trouvé des preuves mitigées d'effets synergiques (12) : alors que les groupes en interaction surpassent souvent le membre moyen d'un groupe nominal (faible synergie), ils surpassent rarement le meilleur membre ( forte synergie). Reflétant cette distinction, nous comparons nos groupes en interaction à quatre repères de performance correspondant chacun à un groupe nominal distinct construit en tirant trois individus au hasard et sans remise d'un même bloc. Le premier repère correspond au score de performance d'un membre du groupe nominal choisi au hasard (équivalent à un individu moyen), tandis que les trois autres correspondent à l'individu avec la meilleure performance de phase 1 sur chacune des trois métriques définies ci-dessus (c'est-à-dire, score le plus élevé, durée la plus faible et efficacité la plus élevée). Par conséquent, les groupes nominaux simulent une situation dans laquelle un responsable attribue le travail à un individu au hasard, à l'individu ayant obtenu le score le plus élevé, à l'individu le plus rapide ou à l'individu le plus efficace, à en juger par les performances passées (c'est-à-dire les scores de la phase 1, les durées , et rendements).
Résultats
Performance en fonction de la complexité de la tâche.
Fig. 2 montre comment les performances varient en fonction de la complexité de la tâche. Dans toutes les conditions, une complexité de tâche plus élevée a entraîné des scores normalisés inférieurs (Fig. 2A), une durée plus longue (Fig. 2B) et donc une efficacité moindre (Fig. 2C). Ces tendances de performance sont également valables lorsqu'elles sont mesurées séparément pour les groupes en interaction et nominaux (Annexe SI, section S2 et Fig. S7). En moyenne, les individus et les groupes ont passé environ trois fois plus de temps sur la tâche la plus complexe que sur la tâche la moins complexe, mais ont obtenu des scores normalisés inférieurs d'environ 10 points de pourcentage. Étant donné que les scores normalisés étaient presque toujours supérieurs à 80, cette dernière différence représente environ 50 % de la plage effective, un effet important. La dépendance monotone claire des trois mesures de performance vis-à-vis de la complexité est importante pour deux raisons. Tout d'abord, cela valide notre conception, démontrant que les augmentations de complexité telles que capturées par les changements dans les paramètres de tâche N, M et Q se traduisent de manière directe par la complexité vécue par nos participants. Deuxièmement, il offre un effet de levier considérable pour tester notre prédiction selon laquelle la performance relative des groupes en interaction par rapport aux groupes nominaux dépend de la complexité de la tâche.
Variation de la complexité des tâches d'attribution des salles. L'augmentation de la complexité de la tâche (A) réduit le score normalisé, (B) augmente le temps nécessaire pour terminer la tâche et (C) réduit l'efficacité. Les données sont combinées pour les conditions individuelles et de groupe dans les six blocs. Les barres d'erreur indiquent les intervalles de confiance à 95 % (certains ne sont pas assez grands pour être affichés). Les groupes et les individus ont obtenu au moins 80 % de la note maximale dans plus de 85 % des tâches ; par conséquent, la plage effective du score normalisé (c'est-à-dire l'axe y de A) se situe entre 80 et 100 %. Le temps minimum requis pour qu'une solution soit soumise est de 1 min, et le maximum est de 10 min ; par conséquent, la plage effective pour la durée (c'est-à-dire l'axe y de B) est comprise entre 1 et 10 min. La différence de difficulté éprouvée entre la complexité très faible et la complexité très élevée est très importante : le score normalisé moyen a chuté d'environ 50 % de la fourchette effective des scores (d'environ 95 à 85 % sur une échelle effective de 80 à 100), et le temps moyen augmenté de 200% (de 2 à 6 min).
Preuve de la synergie de groupe.
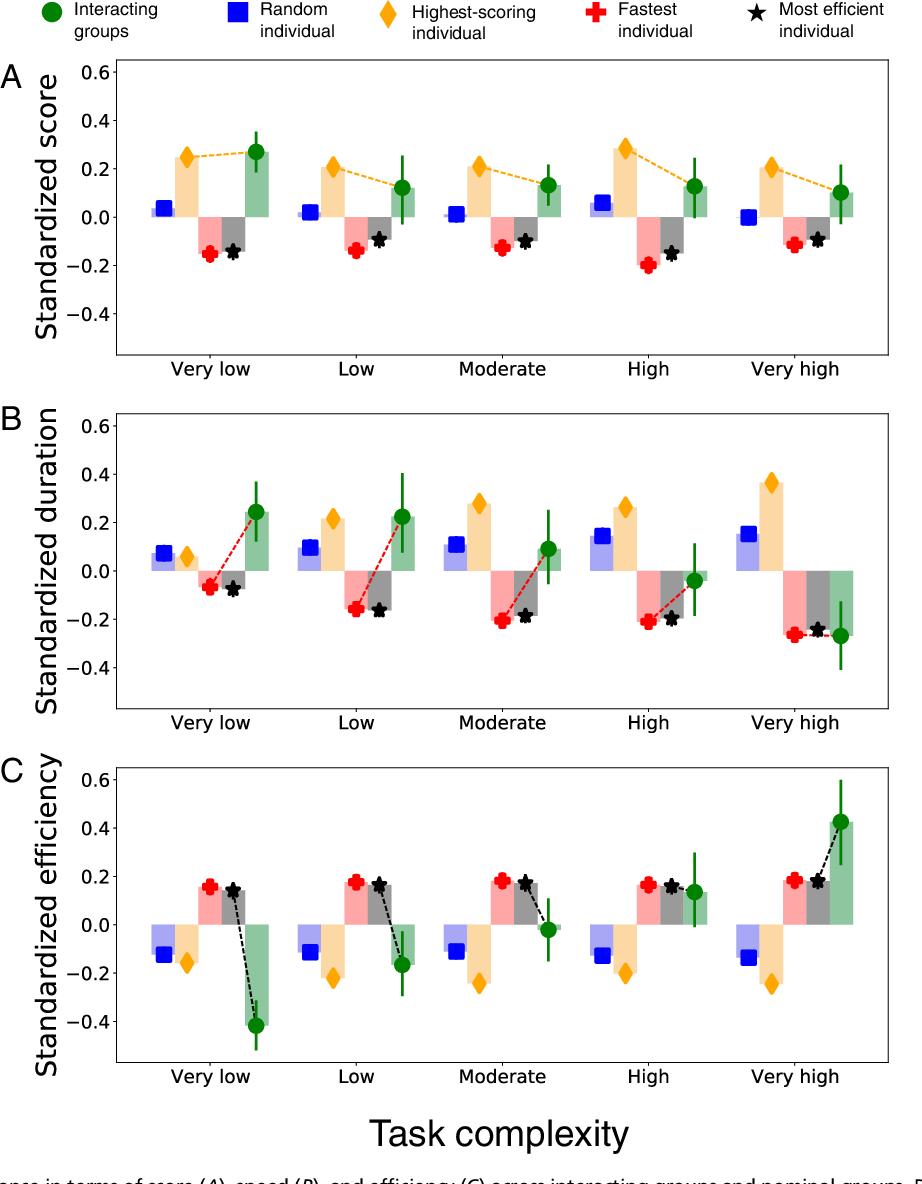
Fig. 3 compare les performances globales du groupe standardisé (transformées en scores z dans chaque niveau de complexité de la tâche) avec les quatre définitions de groupe nominales : individu aléatoire, individu ayant obtenu le score le plus élevé, individu le plus rapide et individu le plus efficace.
Comparer les performances en termes de score (A), de vitesse (B) et d'efficacité (C) entre les groupes en interaction et les groupes nominaux. Les données sont combinées dans les six blocs et normalisées (c'est-à-dire transformées en scores z) dans chaque niveau de complexité de la tâche (les différences sont relatives au sein du niveau de complexité et ne doivent pas être comparées entre les niveaux de complexité). Les barres d'erreur indiquent les intervalles de confiance à 95 %. Nous avons répété les analyses présentées dans cette figure pour chaque bloc, avec des résultats qualitativement similaires (Annexe SI, section S3 et Figs. S8–S10).
La performance en tant que qualité de la solution.
Pour tous les niveaux de complexité de la tâche, la Fig. 3A montre que les groupes obtiennent des scores plus élevés que les membres sélectionnés au hasard, les plus rapides et les plus efficaces de groupes nominaux de taille équivalente ( P = 0,013, IC à 95 % [0,026, 0,225] ; P < 0,001, IC à 95 % [0,184, 0,410] ; P < 0,001, IC à 95 % [0,155, 0,378] ; respectivement) mais inférieur au score le plus élevé membre (P = 0,047, IC à 95 % [−0,159, −0,001] ; voir l'annexe SI, tableaux S4 à S7, pour les tableaux de régression). Ce résultat est cohérent avec les découvertes de longue date (33⇓⇓⇓–37) selon lesquelles les groupes en interaction surpassent souvent les groupes nominaux en termes de qualité de la solution lorsque la norme est définie par un critère de membre moyen (faible synergie), mais pas lorsqu'elle est définie par un critère de meilleur membre (forte synergie).
Performance comme vitesse.
Fig. 3B montre que les groupes en interaction accomplissent des tâches plus complexes, mais pas plus simples, plus rapidement que les membres aléatoires et les plus performants de groupes nominaux de taille équivalente. De plus, les groupes en interaction sont aussi rapides que les membres les plus rapides et les plus efficaces à la complexité de la tâche la plus élevée (voir l'annexe SI, les tableaux S8 à S10, pour les tableaux de régression). Ceux-ci suggèrent qu'en effet, pour les tâches avec de nombreuses composantes (étudiants et salles) et des interdépendances denses (de nombreuses contraintes), les avantages de la distribution du travail à un groupe pourraient l'emporter sur les pertes de processus associées aux groupes en interaction, ce qui est cohérent avec les résultats des travaux antérieurs ( 36).
Performance comme efficacité.
Enfin, la Fig. 3C montre que pour les tâches les plus complexes les gains de vitesse dépassent les déficits de score. Il en résulte une interaction frappante entre la complexité de la tâche et l'organisation du travail : alors que les groupes en interaction sont considérablement moins efficaces que les membres sélectionnés de groupes nominaux sur des tâches simples, leur efficacité relative augmente avec la complexité de la tâche jusqu'à ce qu'ils dépassent les scores les plus élevés, les plus rapides et les plus efficaces. membres à la complexité la plus élevée (voir l'annexe SI, les tableaux S11 à S13, pour les tableaux de régression). Ce résultat rappelle la prise de décision de groupe chez les insectes sociaux dans laquelle une étude récente a montré que les colonies de fourmis surpassent les fourmis individuelles lorsque la tâche de discrimination est difficile mais pas lorsqu'elle est facile (38).
Déballer la synergie de groupe.
La découverte selon laquelle les groupes en interaction sont plus efficaces que les meilleurs membres sélectionnés de groupes nominaux de taille équivalente, selon l'une de nos quatre définitions, lorsque la tâche est complexe, mais pas lorsque la tâche est simple, suggère que l'équilibre entre les pertes de processus et les gains synergiques dépend de la complexité de la tâche. Pour mieux comprendre cette dépendance, et en notant que la variation d'efficacité apparente dans (Fig. 2C) est plus dépendante de la variation de la durée de la tâche (qui varie entre 2 et 6 min en moyenne, Fig. 2B) que de la variation du score atteint (qui varie entre 95% et 85% en moyenne, Fig. 2A), nous présentons ensuite une analyse exploratoire du temps passé à chaque étape de résolution de la tâche. Cette analyse est rendue possible par la nature très granulaire de nos données. Étant donné que chaque action entreprise par chaque participant est horodatée, nous pouvons diviser le temps de résolution global en segments mesurés très précisément qui correspondent à des étapes distinctes du processus de résolution de problèmes. Pour plus de clarté, nous définissons quatre segments clés, illustrés schématiquement sur la figure 4A :
Jalons d'achèvement des tâches. (A) Les quatre étapes du processus de résolution de problèmes : (i) la première solution intermédiaire est générée, (ii) la meilleure solution intermédiaire est générée, (iii) la solution finale est générée et (iv) la solution finale est soumis. (B, D, F et H) Le temps passé (en minutes) par les groupes et les individus (qu'ils soient aléatoires, avec le score le plus élevé, le plus rapide ou le plus efficace) dans chaque segment de temps. (C, E, G et I) Le temps standardisé passé (transformé en scores z ; c'est-à-dire montrant la différence relative au sein du niveau de complexité) dans chaque segment de temps. Les barres d'erreur indiquent les intervalles de confiance à 95 %.
Délai jusqu'à la première solution, .
Le temps entre le début de la tâche et la génération de la première solution peut être considéré comme le temps passé à formuler une stratégie pour aborder la tâche.
Délai pour la meilleure solution, .
La meilleure solution n'est pas nécessairement celle soumise car l'instance de tâche ne se termine qu'une fois qu'un groupe/individu décide de soumettre une solution, et les groupes/individus peuvent générer des solutions après leur meilleure solution sans y revenir.
Délai entre la meilleure solution et la solution finale, .
Le temps passé entre la génération de la meilleure solution et la solution finale, qui peut être considéré comme une "exploration excessive", diminue l'efficacité car elle conduit à une qualité de solution inférieure (ou égale) mais à une durée totale de tâche plus longue.
Délai entre la solution finale et la soumission, .
Le temps passé entre la génération de la solution finale et la décision de la soumettre, qui peut être considéré comme " temps d'engagement », peut être une autre source d'inefficacité car elle conduit à une qualité de solution égale mais augmente la durée totale de la tâche.
Fig. 4 montre deux ensembles de comparaisons entre groupes en interaction et nominaux pour chacun de ces quatre segments. Les figures 4 B, D, F et H montrent les durées brutes pour , , et
Premièrement, nous observons que (en moyenne) les groupes en interaction passent moins de temps en (temps jusqu'à la première solution, Fig. 4 B et C) que les membres des groupes nominaux quelle que soit la complexité de la tâche ( pour tous ; et annexe SI, tableau S14). Nous supposons que cette observation peut être liée aux arguments d'études récentes selon lesquels l'appartenance à un groupe réduit le sens des responsabilités et le regret auxquels les membres peuvent être confrontés individuellement dans les mêmes circonstances. Si elle est correcte, une barrière émotionnelle réduite à l'action peut être un mécanisme sous-jacent poussant les membres du groupe à agir plus tôt (39).
Deuxièmement, nous observons un effet notable de la complexité des tâches sur (temps jusqu'à la meilleure solution, Fig. 4 D et E) : les groupes qui interagissent sont plus lents à atteindre leur meilleure solution que les plus rapides et les membres les plus efficaces des groupes nominaux pour la tâche la moins complexe mais plus rapides pour la tâche la plus complexe (P < 0,001, IC à 95 % [0,119, 0,385] et [0,109, 0,371], respectivement, à la complexité la plus faible, et P < ; 0,001, IC à 95 % [−0,351, −0,085] et [−0,370, −0,108], respectivement, à la complexité la plus élevée ; voir les tableaux S17 à S18 de l'annexe SI pour les tableaux de régression). Fait important, nous notons que la majeure partie de la durée des tâches est consacrée à ce segment, ce qui suggère que la rapidité de la meilleure solution est le principal contributeur à la synergie de groupe. Une explication potentielle de la raison pour laquelle les groupes en interaction sont plus rapides à trouver la meilleure solution à une complexité élevée est que les groupes en interaction réalisent certains avantages de la division du travail (voir l'annexe SI, section S4 et la figure S11, pour des preuves suggestives). Une autre explication possible, pour laquelle nous voyons des preuves anecdotiques dans les journaux de discussion (Annexe SI, Fig. S11), est que les groupes en interaction sont plus disposés à satisfaire en acceptant une solution actuellement disponible comme satisfaisante (40). Une autre encore pourrait être qu'ils bénéficient du tour de rôle, dans lequel une personne est principalement active, tandis que les autres envisagent leur(s) prochain(s) mouvement(s). Malheureusement, la conception actuelle de l'expérience ne nous permet pas de faire la distinction entre ces explications alternatives, elles restent donc spéculatives.
Troisièmement, nous observons qu'indépendamment de la complexité, les groupes en interaction passent plus de temps dans le segment (exploration excessive, Fig. 4 F et G) par rapport aux membres des groupes nominaux ; comme pour , la différence est constante à tous les niveaux de complexité (voir l'annexe SI et les tableaux S19 à S20 pour les tableaux de régression). Quatrièmement, les groupes en interaction passent également plus de temps à s'engager dans une solution () que les membres sélectionnés des groupes nominaux, là encore quelle que soit la complexité (Fig. 4 H et I et SI Annexe, Tableau S14) . Nous supposons que le fait que des groupes en interaction puissent communiquer via le chat (et qu'ils n'aient pas de leader désigné) peut ajouter de la pression sur les groupes pour s'assurer que leurs décisions sont prises collectivement (c'est-à-dire parvenir à un consensus), ce qui pourrait contribuer à l'effet observé.
Cinquièmement, nous observons que la durée totale moyenne des tâches varie de min à très faible complexité à min à très haute complexité (sur un maximum de 10 min), ce qui signifie que les participants soumettent généralement la solution et terminent l'instance de tâche avant de manquer de temps. Cette observation est pertinente pour notre analyse dans la mesure où nos comparaisons de performances de groupes en interaction avec celles de membres sélectionnés de groupes nominaux ne sont pas affectées par la contrainte de temps.
En résumé, la figure 4 révèle deux types de pertes de processus (c'est-à-dire le temps supplémentaire consacré à l'exploration excessive et à la recherche d'un consensus) et deux types de synergies (c'est-à-dire un délai plus rapide pour la première solution et un délai plus rapide pour la meilleure solution pour des tâches complexes ). Fait intéressant, alors que les synergies, en particulier dans le délai de la meilleure solution, dépendent de la complexité des tâches, les pertes de processus ne le sont pas. En d'autres termes, nos résultats suggèrent qu'être dans un groupe en interaction a des coûts fixes qui sont relativement cohérents à travers les niveaux de complexité des tâches, mais un avantage qui varie selon les niveaux de complexité (c'est-à-dire moins de temps passé à trouver la meilleure solution).
Pour clarifier davantage ce résultat, nous agrégeons ensuite les coûts et les avantages afin de quantifier la valeur de l'exécution de la tâche dans un groupe en interaction à tous les niveaux de complexité. En particulier, nous mesurons chaque coût et bénéfice comme la différence absolue, en termes de temps passé, entre les groupes en interaction et le membre aléatoire (c'est-à-dire moyen) des groupes nominaux dans chaque segment de temps :
Fig. 5 montre que le coût total associé aux inefficacités de groupe en interaction (c. Cela explique notre découverte selon laquelle les groupes sont plus efficaces que les membres les plus performants, les plus rapides et les plus efficaces de groupes nominaux de taille équivalente lorsque la tâche est complexe, mais que cette relation est inversée lorsque la tâche est simple. Nous trouvons des résultats similaires pour la comparaison des membres les mieux notés (Annexe SI, section S5 et Fig. S12).
Le rapport coût-bénéfice des groupes en interaction. La figure illustre la différence absolue en termes de temps moyen passé entre des groupes en interaction et un groupe nominal individuel moyen dans chaque segment de temps.
Exploration des différences dans les approches de résolution de problèmes.
Pour récapituler nos principaux résultats, les groupes en interaction sont plus efficaces que même le membre le plus efficace des groupes nominaux pour les problèmes très complexes ; par conséquent, nous concluons qu'ils affichent une forte synergie pour l'efficacité (Fig. 3C). En ce qui concerne la vitesse, les groupes en interaction sont plus rapides que le membre moyen (choisi au hasard) et aussi rapides que le membre le plus rapide de groupes nominaux de taille équivalente (Fig. 3B), affichant ainsi une faible synergie. Pour la qualité de la solution, les groupes en interaction affichent une synergie encore plus faible car ils obtiennent un score plus élevé que le membre moyen mais pas tout à fait aussi bien que le membre le plus élevé des groupes nominaux (Fig. 3A).
Pour approfondir ces résultats, nous avons examiné le nombre et le rythme des solutions intermédiaires générées, où une solution intermédiaire est définie comme une affectation d'étudiants à des salles (c'est-à-dire que chaque action entreprise par un participant génère une solution intermédiaire). Comme le montrent les figures 6 A et B, nous observons que les groupes ont non seulement généré plus de solutions intermédiaires que les membres aléatoires, les plus performants, les plus rapides et les plus efficaces de groupes nominaux de taille équivalente ( pour tous, IC à 95 % , , et respectivement ; annexe SI, tableau S23) ; ils l'ont également fait à un taux plus élevé ( pour tous, IC à 95 % , , , et , respectivement ; annexe SI, tableau S23). Les groupes en interaction présentaient également un rayon de solution plus large, défini comme la distance d'édition maximale (c'est-à-dire le nombre de différences dans les affectations des étudiants/salles) entre la première solution complète (c'est-à-dire tous les étudiants affectés aux salles mais les conflits peuvent être non résolus) et tous les suivants solutions complètes, ce qui suggère qu'ils ont exploré l'espace des solutions plus largement (Fig. 6C ; pour tous, IC à 95 % , , et respectivement ; annexe SI, tableau S23). Nous avons également confirmé cette conclusion qualitative en utilisant deux autres mesures d'exploration : le pourcentage de solutions à une distance d'édition de deux de la solution finale et le pourcentage de solutions intermédiaires impliquant une violation de contrainte (Annexe SI, Figs. S13 et S14).
Différences mécaniques dans les approches de résolution de problèmes entre les groupes et les individus en interaction. Les groupes en interaction génèrent (A) plus de solutions, (B) à un rythme plus rapide et (C) explorent plus largement l'espace des solutions. (D) Cependant, la qualité de la meilleure solution trouvée (qu'elle soit soumise ou non) n'est pas meilleure que la solution trouvée par les groupes nominaux individuels les mieux notés. Les barres d'erreur indiquent les intervalles de confiance à 95 %.
À la lumière de ces observations, il est d'autant plus surprenant que les groupes en interaction n'aient pas trouvé de solutions de meilleure qualité que le membre ayant obtenu le score le plus élevé des groupes nominaux (Fig. 6D ; ; Annexe SI, Tableau S23). L'écart peut en partie s'expliquer par le fait que les groupes en interaction omettent également de soumettre leur solution la mieux trouvée à un taux plus élevé que l'individu ayant obtenu le score le plus élevé : dans toutes les complexités, l'individu ayant obtenu le score le plus élevé ne soumet pas sa solution la mieux trouvée
Qu'est-ce qui pourrait expliquer la combinaison d'une forte synergie en termes d'efficacité et d'une faible synergie en termes de qualité et de rapidité des solutions ? Des recherches antérieures qui conceptualisent la résolution de problèmes comme une recherche adaptative sur un paysage de performance robuste (14, 27), dans laquelle chaque point du paysage représente une solution à l'affectation de la pièce et la hauteur du point représente la performance de cette affectation, fournit plusieurs, explications éventuellement interdépendantes. Une explication potentielle est que les individus les mieux notés ont de meilleures représentations (approximations de dimension inférieure) du véritable paysage de performance, ce qui leur permet d'évaluer les solutions (et les trajectoires de solution) hors ligne sans les tester par l'expérimentation (41, 42). De meilleures représentations peuvent conduire à des évaluations hors ligne plus précises et à des efforts de recherche plus efficaces (26, 43, 44), caractérisés par moins de solutions intermédiaires et une meilleure qualité de solution. Alternativement, des groupes de résolveurs de problèmes peuvent avoir des intérêts contradictoires (par exemple, maximiser le score par rapport à minimiser la durée) et, par conséquent, des visions différentes du bon plan d'action (45). Si cela est vrai, les groupes pourraient bénéficier d'une coordination centrale en désignant un chef de groupe (45) ou d'interventions liées au processus, comme l'imposition de pauses intermittentes dans l'interaction (46, 47). Une autre possibilité est que lorsque le temps est limité, les stratégies de recherche qui permettent des gains rapides (c'est-à-dire des améliorations de performances considérables dès le début) et réduisent la quantité d'exploration peuvent sembler supérieures (26). Par conséquent, alors que la stratégie de recherche locale d'approfondissement du chemin (par exemple, l'escalade) adoptée par les membres les plus performants de groupes nominaux de taille équivalente pourrait offrir des avantages de performance à court terme, la stratégie des groupes en interaction consistant à élargir le domaine de recherche pourrait être plus avantageuse à long terme (48, 49).
Discussion
Pour de nombreuses tâches d'intérêt, les responsables peuvent décider d'attribuer une tâche à un groupe en interaction ou à un nombre comparable d'individus travaillant de manière indépendante (12). Pour des paramètres tels que ceux-ci, nos résultats offrent plusieurs informations. Tout d'abord, les décisions sur la façon d'allouer le travail - à des groupes en interaction ou à des groupes nominaux - doivent dépendre de la complexité de la tâche à accomplir et de la manière dont la performance est évaluée. Par exemple, si un responsable souhaitait trouver une solution viable à un CSOP en un minimum de temps, la recommandation serait de demander à un groupe de résoudre le problème lorsque le problème est complexe, mais de demander à des résolveurs de problèmes indépendants lorsqu'il est simple. Il convient de noter que les résultats de durée et d'efficacité présentés ici peuvent en fait sous-estimer la manière dont cela fonctionnerait dans la pratique. Par exemple, si le travail était organisé en groupes nominaux, cet arrangement produirait toujours plusieurs solutions différentes entre lesquelles un responsable pourrait choisir. Bien que notre opérationnalisation des groupes nominaux ait simulé une situation dans laquelle le manager prend la décision instantanément, il existe des circonstances où un manager pourrait vouloir considérer les mérites des différentes solutions, et cela prendrait un temps non nul. Ce n'est pas le cas des groupes en interaction, où le processus de décision est déjà inclus dans le temps écoulé de l'exercice de résolution de problèmes.
Deuxièmement, nos résultats suggèrent également qu'une explication possible de la raison pour laquelle les pertes de processus de groupe ont figuré plus en évidence dans les résultats de recherche que les gains synergiques (12) est que les études en laboratoire sur les performances de groupe reposent généralement sur des tâches très simples. En effet, les preuves de laboratoire les plus claires à ce jour pour une performance de groupe supérieure, bien que rares, proviennent de groupes travaillant sur des tâches relativement complexes (13, 46, 50, 51) ; cependant, le fait que la complexité des tâches ne varie pas systématiquement au sein d'une même étude représente une source majeure de variation incontrôlée dans les recherches antérieures (17, 36).
Troisièmement, notre analyse de la façon dont les groupes en interaction et les individus indépendants diffèrent dans le temps qu'ils passent à différentes étapes du processus de résolution de problèmes offre un aperçu de la manière dont les processus de groupe pourraient être améliorés. Par exemple, notre constatation selon laquelle les groupes passent plus de temps à décider qu'une tâche a été accomplie (c. , améliorant ainsi les performances du groupe. De plus, notre constatation selon laquelle les groupes en interaction sont moins susceptibles de soumettre leur meilleure solution trouvée suggère que le stockage de leurs meilleures solutions afin qu'elles puissent être rechargées et potentiellement modifiées dans les étapes suivantes (une caractéristique omniprésente des logiciels de productivité personnelle) devrait également améliorer leurs performances ( 46).
Quatrièmement, notre analyse de la dynamique de solution des groupes par rapport aux individus provoque des énigmes supplémentaires pour les travaux futurs. En particulier, si les groupes génèrent plus de solutions plus rapidement et plus efficacement sur une plage plus large de l'espace de solutions que même les individus les mieux notés, pourquoi ne trouvent-ils pas de meilleures solutions ?
Enfin, nous concluons que la science de la performance de groupe bénéficierait d'une appréciation plus approfondie et plus systématique des similitudes et des différences entre les tâches que les groupes sont invités à effectuer, à la fois en laboratoire et sur le terrain. Il est nécessaire de disposer d'une théorie complète et empiriquement fondée sur les tâches de groupe (12). Un programme de recherche qui variait systématiquement les types de tâches ainsi que les processus de groupe autorisés et d'autres facteurs contextuels ferait progresser la science fondamentale de la résolution de problèmes de groupe tout en abordant également les applications pratiques.
Matériels et méthodes
L'étude a été examinée par le Microsoft Research Ethics Advisory Board et approuvée par le Microsoft Research Institutional Review Board (MSR IRB ; Approval 0000019). Tous les participants ont donné leur consentement explicite pour participer à cette étude, et le MSR IRB a approuvé la procédure de consentement. Notre conception expérimentale, la taille de l'échantillon et les analyses comparant les performances des groupes en interaction et des groupes nominaux ont été préenregistrées avant la collecte des données (AsPredicted 13123). Toutes les autres analyses sont exploratoires.
Algorithmic Solver.
Nous avons modélisé chaque problème d'attribution de salle comme un problème de programmation à nombre entier mixte et avons généré le temps d'exécution pour que les ordinateurs résolvent chaque problème à l'aide du logiciel IBM ILOG CPLEX Optimization Studio, qui est un solveur de programmation mathématique hautes performances pour la programmation linéaire, la programmation en nombres entiers mixtes et la programmation quadratique. Le logiciel fonctionnait sur un ordinateur portable avec un microprocesseur Intel Core i5 fonctionnant à une vitesse de 2,6 GHz. Nous avons exécuté le logiciel en utilisant la configuration par défaut des paramètres. L'unité de temps d'exécution dans le fichier de tâche est « ticks », qui est l'unité de CPLEX pour mesurer la quantité de travail effectuée. La correspondance des ticks au temps d'horloge varie selon les plates-formes (y compris le matériel, les logiciels, la charge de la machine, etc.), mais étant donné un problème de programmation à nombre entier mixte et les paramètres, les ticks nécessaires pour résoudre un problème sont déterministes. En ce sens, la fiabilité test-retest du solveur algorithmique est de 1. Voir l'annexe SI, section 1.4.2, pour plus de détails.
Analyse statistique.
Étant donné que chaque groupe (ou individu) en interaction a effectué les cinq tâches d'attribution de salle, nous avons effectué des tests pour les différences entre les conditions au niveau de la tâche. Pour les effets d'interaction, nous avons modélisé les données à l'aide d'un modèle mixte linéaire généralisé pour chaque résultat (par exemple, score, durée et efficacité) avec un effet aléatoire pour le groupe ou l'identifiant individuel. Ces modèles tiennent compte de la structure imbriquée des données. Tous les tests statistiques étaient bilatéraux (conformément à notre préinscription). Les détails des tests statistiques se trouvent dans l'annexe SI, section S7.
Coefficients standardisés.
Pour permettre des comparaisons significatives des tailles d'effet entre les tâches de différents niveaux de complexité, nous normalisons diverses mesures de performance (par exemple, le score, la durée, l'efficacité et le nombre de solutions) dans chaque niveau de complexité. Par exemple, la valeur standardisée de la mesure X, mesurée pour l'instance de tâche i de complexité c, est définie commeoù
Disponibilité des données
Les données et le code de réplication sont disponibles sur Harvard Dataverse, https://doi.org/10.7910/DVN/RP2OCY (52). L'expérience a été développée à l'aide de la plate-forme Empirica (53). Le code source de la tâche d'attribution de salle se trouve sur https://github.com/amaatouq/room-assignment-csop, et le code source du test Reading the Mind in the Eyes se trouve sur https://github .com/amaatouq/rme-test.
Remerciements
Nous remercions Valery Yakubovich, Hazhir Rahmandad et James Houghton pour leurs discussions et leurs commentaires utiles. Les auteurs remercient la Fondation Alfred P. Sloan (G-2020-13924) pour son soutien financier.
Notes de bas de page
Contributions des auteurs : A.A., M.Y. et D.J.W. recherche conçue; A.A., M.Y. et D.J.W. effectué des recherches ; A.A., M.A., M.Y. et D.J.W. apporté de nouveaux réactifs/outils analytiques ; A.A., M.A., M.Y. et D.J.W. données analysées ; et A.A., M.A., M.Y. et D.J.W. a écrit le papier.
Les auteurs ne déclarent aucun intérêt concurrent.
Cet article est une soumission directe PNAS.
Cet article contient des informations complémentaires en ligne sur https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2101062118/-/DCSupplemental.
Cet article en libre accès est distribué sous Creative Commons Attribution-NonCommercial-NoDerivatives License 4.0 (CC BY-NC-ND).




