Tehtävän monimutkaisuus vähentää ryhmäsynergiaa Tehtävän monimutkaisuus vähentää ryhmäsynergiaa

Merkitys

Sekä tutkijoita että johtajia on askarruttanut kysymys siitä, menestyvätkö vuorovaikutuksessa olevat ongelmanratkaisijat itsenäisiä yksilöitä paremmin, ja jos on, millä ehdoilla. Tässä kuvaamme koetta, jossa yksilöitä ja ryhmiä arvioitiin sarjassa vaihtelevan monimutkaisia tehtäviä. Huomaamme, että ryhmät ovat yhtä nopeita kuin nopein yksilö ja tehokkaampia kuin tehokkain yksilö, kun tehtävä on monimutkainen, mutta ei silloin, kun tehtävä on yksinkertainen. Sen jälkeen kvantifioimme tarkasti vuorovaikutuksessa oleviin ryhmiin liittyvät synergistiset voitot ja prosessihäviöt ja huomaamme, että näiden kahden välinen tasapaino riippuu monimutkaisuudesta. Tutkimuksemme pystyy sovittamaan yhteen ristiriitaiset havainnot ryhmäsynergiasta aikaisemmassa työssä.

Abstrakti

Monimutkaisuus – joka määritellään komponenttien lukumäärän ja niiden välisten keskinäisten riippuvuuksien luonteen perusteella – on selvästi olennainen piirre kaikissa ryhmien suorittamissa tehtävissä. Tehtävän monimutkaisuuden rooli ryhmän suorituskyvyn määrittämisessä on kuitenkin edelleen huonosti ymmärretty, osittain siksi, että ei ole olemassa selkeää kieltä ilmaistakseen monimutkaisuutta tavalla, joka mahdollistaa tehtävien välisen suoraviivaisen vertailun. Tässä vältämme tämän analyyttisen vaikeuden tunnistamalla luokan tehtäviä, joiden monimutkaisuutta voidaan muuttaa systemaattisesti pitäen samalla kaikki muut tehtävän elementit ennallaan. Testaamme sitten tehtävän monimutkaisuuden vaikutuksia ennakkoon rekisteröidyssä kaksivaiheisessa kokeessa, jossa 1 200 henkilöä arvioitiin sarjassa vaihtelevan monimutkaisia tehtäviä (vaihe 1) ja jaettiin sitten satunnaisesti ratkaisemaan samanlaisia tehtäviä joko vuorovaikutuksessa olevissa ryhmissä tai itsenäisinä yksilöinä ( vaihe 2). Huomaamme, että vuorovaikutuksessa olevat ryhmät ovat yhtä nopeita kuin nopein yksilö ja tehokkaampia kuin tehokkain yksilö monimutkaisiin tehtäviin, mutta eivät yksinkertaisempiin. Hyödyntämällä erittäin rakeista digitaalista dataamme, määrittelemme ja mittaamme tarkasti ryhmäprosessien häviöt ja synergistiset hyödyt ja näytämme, että näiden kahden kytkimen välinen tasapaino merkitsee tehtävän monimutkaisuuden väliarvoja. Lopuksi havaitsemme, että vuorovaikutuksessa olevat ryhmät luovat enemmän ratkaisuja nopeammin ja tutkivat ratkaisuavaruutta laajemmin kuin itsenäiset ongelmanratkaisijat ja löytävät laadukkaampia ratkaisuja kuin kaikki paitsi eniten pisteitä saaneet yksilöt.

Vuorovaikutteisten ongelmanratkaisijoiden ryhmien suorittamat tehtävät – joko todellisessa maailmassa tai kokeellisissa olosuhteissa – vaihtelevat useiden ulottuvuuksien mukaan, jotka vaikuttavat uskottavasti ryhmän suorituskykyyn (1⇓⇓⇓⇓–6). Tässä artikkelissa keskitymme tehtävien tärkeään, mutta empiirisesti alitutkituun ulottuvuuteen, monimutkaisuuteen, jonka ymmärretään yleensä riippuvan ainakin kahdesta tekijästä: (i) tehtävän muodostavien erillisten komponenttien lukumäärästä ja (ii) määrästä, vahvuudesta. , ja näiden komponenttien keskinäisten riippuvuuksien konfigurointi (7⇓⇓⇓–11).

Intuitiivisesti tehtävien monimutkaisuus on ilmeisen tärkeää ryhmän suorituskyvyn kannalta. Kaikki muu on sama, ongelmanratkaisijoiden voisi odottaa suoriutuvan huonommin tehtävissä, joissa on enemmän komponentteja tai joissa komponenttien välinen vuorovaikutus on tiheämpää. Lisäksi voidaan myös olettaa, että tehtävän monimutkaisuus vaikuttaa ryhmän "synergiaan", joka määritellään suorituskyvyksi, joka ylittää sen, mitä voitaisiin odottaa samankokoiselta itsenäisesti työskentelevien henkilöiden joukolta – eli "nimellisryhmältä" (12). Tässä tapauksessa on kuitenkin vähemmän ilmeistä, mikä vaikutuksen suunta olisi. Toisaalta vuorovaikutuksessa olevat ryhmät voivat menestyä paremmin kuin nimelliset ryhmät monimutkaisissa tehtävissä, koska ne pystyvät jakamaan vaivaa (13), jakamaan tietoa laadukkaista ratkaisuista (14) tai korjaamaan virheitä (15). Toisaalta monimutkaisemmissa tehtävissä vuorovaikutuksessa olevat ryhmät voivat kokea vieläkin suurempia prosessihäviöitä – mukaan lukien sosiaalinen löystyminen (16), ryhmäajattelu (17) ja ihmisten välinen konflikti (4) – mahdollisesti siksi, että monimutkaiset tehtävät asettavat yksittäisille osallistujille enemmän vaatimuksia ja tarjoavat enemmän enemmän mahdollisuuksia juuttua globaalisti alioptimaalisiin paikallisiin optimeihin, joista kumpi tahansa voi myös johtaa lisääntyneeseen stressiin ja alitulokseen verrattuna nimellisryhmiin.

Suuri haaste tehtävien monimutkaisuuden vaikutuksia koskevien kysymysten ratkaisemisessa on se, että vaikka korkean tason konsepti vaikuttaa intuitiiviselta, sitä ei ole vielä otettu käyttöön tarpeeksi tarkasti, jotta tutkijat voisivat kvantifioida erityyppisten tehtävien monimutkaisuutta ja siten tehdä omenoita. omenoihin niiden välisiä vertailuja. Pikemminkin olemassa olevat operaatiot ovat usein itsessään monimutkaisia. Esimerkiksi yksi malli listaa 27 monimutkaisuutta edistävää tekijää ryhmiteltynä 10 monimutkaisuusulottuvuuden alle (9), kun taas muut mallit ovat riittävän aluekohtaisia, joten numeerisia eroja erityyppisten tehtävien välillä on vaikea tulkita (7). Sekaannusta lisää, että jotkut määritelmät korostavat objektiivista monimutkaisuutta viittaamalla vain tehtävän ominaisuuksiin, joita voidaan mitata tehtävän suorittajista riippumatta, kun taas toiset korostavat subjektiivista monimutkaisuutta, tehtävän monimutkaisuutta sen tekevien kokemana (9, 11).

Tässä vältetään nämä analyyttiset vaikeudet tunnistamalla tehtäväluokka, jonka monimutkaisuutta voidaan muuttaa systemaattisesti pitäen samalla kaikki muut tehtävän elementit ennallaan. Tällä tavalla voimme helposti mitata suorituskykyä lisääntyvän monimutkaisuuden funktiona ilman, että tarvitsemme huolta muista tehtävän näkökohdista, kuten tehtävätyypistä (3) tai muista ryhmäprosessien ominaisuuksista (4, 18) johtuvista sekaannuksista. Lisäksi edellytämme, että tehtävämme voidaan realistisesti suorittaa joko itsenäisesti tai yhteistyössä, mikä mahdollistaa suoraviivaisen vertailun nimellisten ja vuorovaikutuksessa olevien ryhmien välillä.

Nämä kriteerit täyttävä tehtäväluokka ovat rajoitusten tyytyväisyys- ja optimointiongelmat (CSOP), joita tutkitaan laajasti tekoäly- ja toimintatutkimuksessa. Yhteys operaatiotutkimukseen on hyödyllinen, koska toisin kuin muut "lelu"-ongelmat, CSOP:t kartoittavat suhteellisen intuitiivisella tavalla erilaisia käytännön resurssien allokointiongelmia ja niitä on käytetty mallintamaan monia käytännön kiinnostavia ongelmia. Esimerkkejä CSOP-ohjelmista ovat henkilöstön palkkaaminen ohjelmistoprojektit, joissa on useita arvioitavia potentiaalisia kehittäjiltä toimintoihin liittyviä toimeksiantoja (19); oppimisryhmien muodostaminen joidenkin yhteistyötavoitteisiin liittyvien kriteerien perusteella (20); rautateiden aikataulut (21); ja jakaa rokotteita, hengityskoneita ja lääketieteellisiä tarvikkeita COVID-19-pandemian aikana (22). Lisäksi vaikka CSOP-harjoitukset taltioivat tärkeitä piirteitä todellisen maailman ryhmän ongelmanratkaisuharjoituksista, ne eivät vaadi osallistujilta erityistaitoja. Tämän seurauksena osallistujia voidaan rekrytoida verkkopalveluista, mikä vähentää ryhmien samanaikaisen osallistumisen koordinoinnin kustannuksia ja vaikeutta. Lopuksi, kuten muissakin monimutkaisissa ongelmissa (14, 23⇓–25), CSOP:n voittofunktiota voidaan kuvata karuksi suorituskykymaisemaksi, jossa jokainen maiseman piste edustaa yhdistelmää mahdollisesti toisistaan riippuvaisia valintoja (ongelman ratkaisu). , kun taas pisteen korkeus edustaa kyseisen yhdistelmän suorituskykyä (26, 27). Siksi CSOP:ille voidaan luonnehtia useita paikallisesti optimaalisia, mutta globaalisti alioptimaalisia ratkaisuja (26, 27), joten ne ovat soveltuvia mahdollisesti useisiin ratkaisustrategioihin ja -tyyleihin ilman yhtä universaalia ylivoimaista strategiaa (28).

Erityinen CSOP, jota tutkimme, on huonetehtäväongelma, jossa osallistujat – joko yksilöinä tai ryhminä – osoittavat N opiskelijaa M huoneeseen, joissa jokaisella opiskelijalla on tietty apuohjelma jokaista huonetta varten (SI-liite, kohta 1.1). Tehtävän tavoitteena on maksimoida opiskelijoiden kokonaishyöty ja samalla kunnioittaa Q-rajoituksia (esim. "Oppilaat A ja J eivät saa jakaa huonetta tai olla vierekkäisissä huoneissa"). Kun tehtävä tehdään ryhmissä, osallistujat voivat kommunikoida tekstipohjaisen chatin kautta ja siirtää eri oppilaita samanaikaisesti, jolloin he voivat halutessaan suorittaa rinnakkaiskäsittelyä. Meidän kannaltamme kriittistä tehtävän monimutkaisuutta voidaan muuttaa systemaattisesti säätämällä vain kolmea avainparametria: oppilaiden lukumäärä $(N)$ , huonemäärä $(M)$ ja rajoitusten määrä $(Q)$ . Tämän tehtävän (ja CSOP:n yleensä) merkittävä etu verrattuna tehtäviin, joita tutkitaan yleisemmin ryhmäsuoritusasetuksissa, on se, että sen monimutkaisuus voidaan kvantifioida ajoajalla, jonka algoritminen ratkaisija tarvitsee löytääkseen optimaalisen ratkaisun. voimme helposti luokitella tehtäväinstanssit monimutkaisuuden mukaan (katso lisätietoja kohdasta Materiaalit ja menetelmät). Kuva 1 havainnollistaa, kuinka monimutkaisuutta voidaan vaihdella huoneen osoitusongelman kahden esiintymän välillä. Vähän monimutkaisessa tapauksessa kuusi opiskelijaa on osoitettava neljään huoneeseen, joihin sovelletaan vain kahta rajoitusta ("B:n ja E:n on oltava naapureita" ja "C ja F eivät voi asua samassa huoneessa"). Erittäin monimutkaisessa tapauksessa 18 opiskelijaa on määrättävä 8 huoneeseen 18 rajoituksen alaisena.

Kuva 1.

Kuva huonetehtävästä. Tehtävä edellytti N opiskelijan määrittämistä M huoneeseen, jotta opiskelijoiden kokonaishyötymäärä maksimoi, joilla jokaisella on tietty apuohjelma jokaiselle huoneelle, samalla kun noudatetaan Q-rajoituksia. Tehtävän monimutkaisuutta kuvaavat opiskelijoiden määrä $(N)$ , vapaana olevien asuntolahuoneiden määrä $(M)$ ja rajoitusten määrä $(Q)$ . (Yläosa) Matala monimutkainen tapaus, jossa kuusi opiskelijaa määrätään neljään huoneeseen kahdella rajoituksella. (Alhaalla) Monimutkainen tapaus, jossa 18 opiskelijaa määrätään 8 huoneeseen 18 rajoituksen alaisena. Katso yksityiskohdat SI-liite, kohta S1.1 ja SI-liite, kuvat S1–S2, kuvakaappauksia tehtäväliittymästä.

Kokeilun suunnittelu

Tässä artikkelissa testaamme hypoteesia, jonka mukaan tehtävän monimutkaisuus hillitsee ryhmän ja yksittäisen ongelmanratkaisun suhteellista suorituskykyä. Tätä varten käsittelemme seuraavaa kysymystä: kuinka tasapaino prosessihäviöiden ja synergististen hyötyjen välillä vuorovaikutuksessa olevissa ryhmissä riippuu tehtävän monimutkaisuudesta?

Kokeilumme eteni kahdessa vaiheessa. Vaiheessa 1 1 200 osallistujaa suoritti yksilöllisesti viisi huonetehtävää: kolme erittäin matalan ja kaksi kohtalaisen monimutkaisuutta (SI-liite, taulukko S1) sekä standardin Reading the Mind in the Eyes -testin (SI-liite, kohta S1.2). ja kuva S3), jota käytetään yleisesti sosiaalisen havainnointikyvyn mittarina ja jota käytettiin useissa viimeaikaisissa tutkimuksissa, jotka koskevat sosiaalista havainnointikykyä ryhmän suorituskykyyn (18, 29⇓⇓-32).

Vaiheen 1 päätyttyä arvioimme kaikki osallistujat taitotason ja sosiaalisen havainnoinnin perusteella, jotta voimme määrittää heidät kokeellisiin lohkoihin vaiheessa 2 (SI-liite, kohta 1.4 ja kuva S4). Ottamalla nämä piirteet huomioon lohkosatunnaisprosessissamme vaiheessa 2, pystyimme varmistamaan, että eri taitotasot ja sosiaalinen havainnointikyky (ja niiden yhdistelmät) olivat tasapainossa ryhmä- ja yksilötyöjärjestelyissä. Lohkosatunnaistuksen päätarkoituksena oli ottaa tilastollisesti harvemmin esiintyviä yhdistelmiä (esim. kaikki ryhmän jäsenet, joilla on korkeat taidot tai korkea sosiaalinen havainnointikyky) yliotantaa, mikä lisäsi kokeidemme tilastollista tehoa. Huomaamme, että keskitymme tässä vuorovaikutteisten ja nimellisten ryhmien vertailuun, ei vuorovaikutteisten ryhmien välisiin koostumuseroihin; näin ollen analyysimme taitotason ja sosiaalisen havainnoinnin vaikutuksista suoritukseen julkaistaan muualla (ennakkoilmoittauksemme mukaan).

Samat 1 200 osallistujaa kutsuttiin osallistumaan vaiheeseen 2, ja ensimmäiset 828 osallistujaa, jotka saapuivat paikalle ja läpäisivät huomiotarkastukset (ennakkoilmoittauksemme mukaan; katso SI-liite, taulukko S2, otoskoot) määrättiin toiseen. viiden huonetehtävän sarja (tehtäväjärjestys oli satunnaistettu), myös vaihtelevan monimutkaisuuden (erittäin pieni, matala, kohtalainen, korkea ja erittäin korkea; SI-liite, taulukko S3 ja kuva S5). Kaikki tehtävät aikakatkaistiin 10 minuutin kohdalla vaiheessa 2, monimutkaisuudesta riippumatta. Kunkin osallistujan vaiheessa 1 mitatun taidon ja sosiaalisen havainnointikyvyn perusteella jaoimme jokaisen yksilön ensin lohkoihin (esim. korkea taito, korkea sosiaalinen havainnointikyky; sekataito, korkea sosiaalinen havainnointikyky jne.). Seuraavaksi kussakin lohkossa osallistujat satunnaistettiin yhteen kahdesta ehdosta: vuorovaikutteisen ryhmän ehto ( $N=591$ osallistujaa, jotka muodostivat 197 ryhmää, joiden koko on 3; 1 ryhmän tiedot ovat epätäydellisiä, mikä johtaa numeroon kelvollisia vuorovaikutteisia ryhmiä oli 196), joissa ryhmän jäsenet ratkaisivat ongelman kollektiivisesti ja pystyivät kommunikoimaan keskenään tekstipohjaisen chatin kautta; ja riippumaton yksilöehto ( $N=237$ osallistujaa; tiedot 3 henkilöltä ovat puutteellisia, mikä johtaa kelvollisten riippumattomien henkilöiden lukumäärään 234), jossa jokainen osallistuja työskenteli hänelle osoitetun tehtävän kanssa yksin. Kaikki tässä esitetyt tulokset ovat kokeen vaiheesta 2.

Suorituskyvyn arviointi.

Task monimutkainen ryhmä taso monimutkaisuus ryhmäsynergia

Vaiheessa 2 käytimme kolmea mittaria suorituskyvyn kaappaamiseen huonetehtävätehtävän ilmentymässä: (1) normalisoitu pistemäärä, joka määritellään tehtäväesiintymässä saatuna todellisena pisteenä jaettuna kyseisen tehtävän suurimmalla mahdollisella pistemäärällä; (2) kesto (tai aika sen valmistumiseen), joka määritellään ajaksi, joka on kulunut tehtävän aloittamisesta ratkaisun toimittamiseen (tai siihen asti, kun tehtävän aikakatkaisu 10 minuutin kohdalla); ja lopuksi (3) tehokkuus, joka määritellään normalisoituna pistemääränä jaettuna kestolla.

Kaikki kolme mittaria ovat luonnollisia suorituskyvyn osoittimia, joita voidaan haluta optimoida joissakin olosuhteissa. Jos aikarajoituksia ei ole, esimerkiksi normalisoitu pistemäärä on ilmeinen ratkaisun laadun mitta. Sitä vastoin kesto on sopiva, kun ongelmanratkaisuaika on tärkeämpää kuin laatu (esim. keksiä nopeasti kohtuullisen hyvä suunnitelma resurssien kohdentamiseksi katastrofiavussa), ja tehokkuus on sopivaa, kun sekä laatu että nopeus ovat tärkeitä (esim. , tuotekehityksessä).

Aiemman työn (12, 33⇓⇓⇓–37) perusteella arvioimme ryhmän suorituskykyä verrattuna ns. nimellisiin ryhmiin, jotka määritellään samankokoiseksi itsenäisten yksilöiden joukoksi. Nimelliset ryhmät ovat hyödyllinen vertailukohta vuorovaikutuksessa oleville ryhmille, koska ne ottavat huomioon ryhmien ja yksilöiden välisen erilaisen resurssien saatavuuden (12); toisin sanoen ne mukautuvat henkisten resurssien määrään, jonka ryhmät voisivat tuoda mukanaan (eli työtunnit) ja matemaattiseen todennäköisyyteen, että ainakin yksi jäsen olisi voinut saavuttaa saman suorituskyvyn. Siten vuorovaikutteisen ryhmän suoritus, joka ylittää nimellisen ryhmän suorituskyvyn, voidaan johtua ryhmän vuorovaikutuksesta, ei suuremmista resursseista.

Yleensä vertailut vuorovaikutuksessa olevien ryhmien ja vastaavankokoisten nimellisten ryhmien välillä ovat löytäneet ristiriitaisia todisteita synergistisista vaikutuksista (12): vaikka vuorovaikutuksessa olevat ryhmät ovat usein suoriutuneet nimellisen ryhmän keskimääräistä jäsentä paremmin (heikko synergia), ne ovat harvoin parempia kuin paras jäsen ( vahva synergia). Tätä eroa heijastaen vertaamme vuorovaikutuksessa olevia ryhmiämme neljään suorituskykyyn, joista jokainen vastaa erillistä nimellistä ryhmää, joka on muodostettu piirtämällä kolme yksilöä satunnaisesti ja ilman korvaamista samasta lohkosta. Ensimmäinen vertailuarvo vastaa satunnaisesti valitun nimellisen ryhmän jäsenen suorituspisteitä (vastaa keskimääräistä yksilöä), kun taas loput kolme vastaavat henkilöä, jolla on paras vaiheen 1 suorituskyky kaikilla kolmella edellä määritellyllä mittarilla (ts. korkein pistemäärä, matalin kesto ja suurin tehokkuus). Nimelliset ryhmät siis simuloivat tilannetta, jossa johtaja antaa työn joko satunnaiselle henkilölle, eniten pisteitä saaneelle henkilölle, nopeimmalle henkilölle tai tehokkaimmille henkilöille aiemman suorituksen (eli vaiheen 1 pisteet, kesto) perusteella arvioituna. ja tehokkuusetuja).

Tulokset

Suorituskyky tehtävän monimutkaisuuden funktiona.

Kuva. Kuva 2 näyttää, kuinka suorituskyky vaihteli tehtävän monimutkaisuuden funktiona. Kaikissa olosuhteissa korkeampi tehtävän monimutkaisuus johti alhaisempiin normalisoituihin pisteisiin (kuva 2A), pitempiin kestoihin (kuva 2B) ja siten alhaisempaan tehokkuuteen (kuva 2C). Nämä suorituskykytrendit pätevät myös, kun ne mitataan erikseen vuorovaikutteisten ja nimellisten ryhmien osalta (SI-liite, osa S2 ja kuva S7). Yksilöt ja ryhmät viettivät keskimäärin noin kolme kertaa niin kauan monimutkaisimpaan tehtävään kuin vähiten monimutkaisimpiin, mutta saivat normalisoidut pisteet, jotka olivat noin 10 prosenttiyksikköä alhaisemmat. Ottaen huomioon, että normalisoidut pisteet olivat lähes aina yli 80, tämä viimeinen ero edustaa noin 50 % tehokkaasta alueesta - suuri vaikutus. Kaikkien kolmen suoritusmittarin selkeä monotoninen riippuvuus monimutkaisuudesta on tärkeä kahdesta syystä. Ensinnäkin se validoi suunnittelumme osoittaen, että tehtäväparametrien N, M ja Q muutosten mukaiset monimutkaisuudet muuttuvat yksinkertaisella tavalla osallistujiemme kokemaan monimutkaisuuteen. Toiseksi se tarjoaa huomattavan vipuvaikutuksen testataksemme ennustettamme, jonka mukaan vuorovaikutuksessa olevien ryhmien suhteellinen suorituskyky suhteessa nimellisiin ryhmiin riippuu tehtävän monimutkaisuudesta.

Kuva 2.

Huonevaraustehtävän monimutkaisuuden vaihtelu. Tehtävän monimutkaisuuden lisääminen (A) vähentää normalisoitua pistemäärää, (B) lisää tehtävän suorittamiseen tarvittavaa aikaa ja (C) vähentää tehokkuutta. Tiedot yhdistetään sekä yksittäisten että ryhmien ehdoista kaikissa kuudessa lohkossa. Virhepalkit osoittavat 95 %:n luottamusvälit (jotkut eivät ole tarpeeksi suuria näytettäväksi). Ryhmät ja yksilöt saivat vähintään 80 % maksimipistemäärästä yli 85 %:ssa tehtävistä; näin ollen tehollinen alue normalisoidulle pisteelle (eli A:n y-akselille) on 80 - 100 %. Ratkaisun toimittamiseen vaadittava vähimmäisaika on 1 min ja enimmäisaika 10 min. täten keston tehollinen alue (eli B:n y-akseli) on 1 - 10 min. Ero koetun vaikeuden välillä erittäin alhaisen ja erittäin suuren monimutkaisuuden välillä on erittäin suuri: keskimääräinen normalisoitu pistemäärä laski noin 50 % tehokkaasta pistemäärästä (noin 95 prosentista 85 prosenttiin tehokkaalla asteikolla 80 - 100), ja Keskimääräinen käytetty aika kasvoi 200 % (2 minuutista 6 minuuttiin).

Todisteet ryhmäsynergiasta.

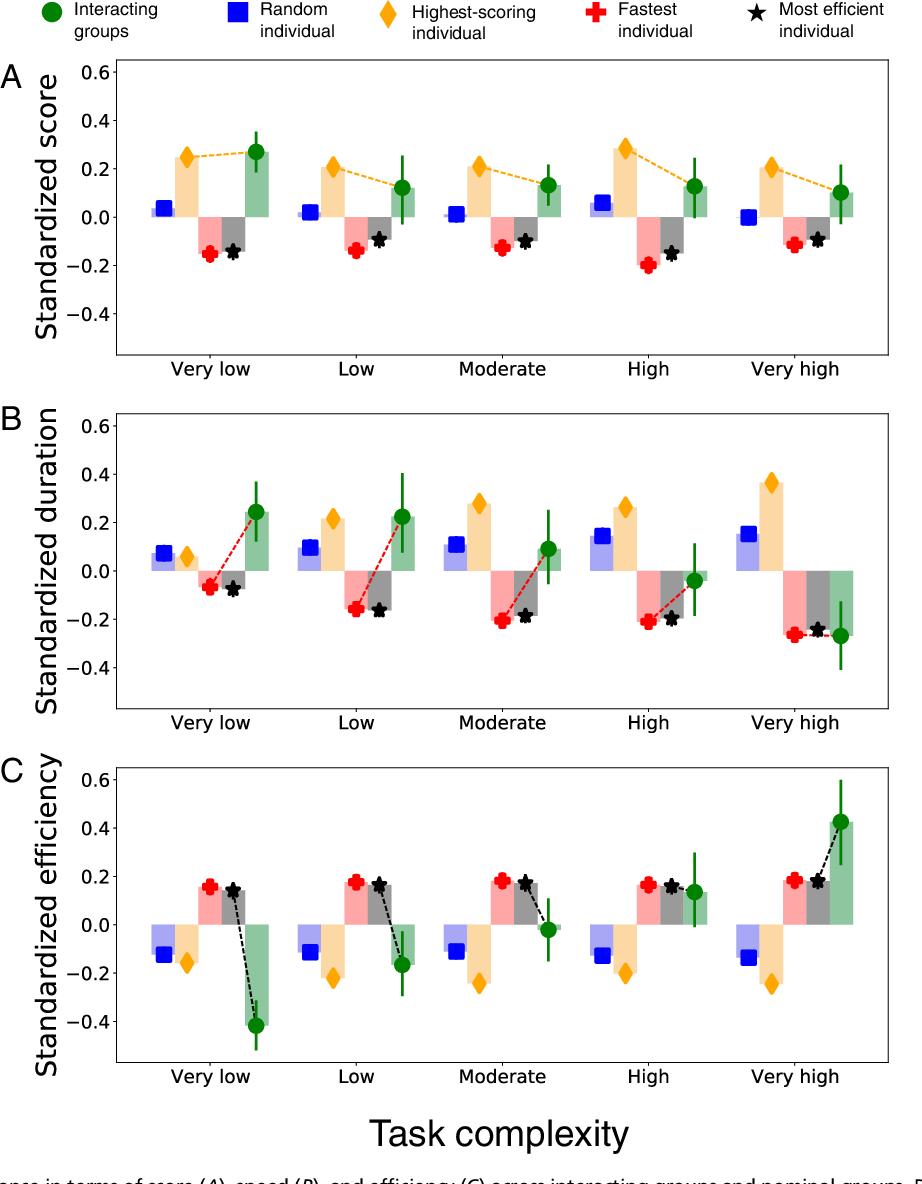
Kuva. 3 vertaa yleistä standardoitua ryhmän suorituskykyä (muunnettu z-pisteiksi kunkin tehtävän monimutkaisuustason sisällä) neljään nimelliseen ryhmämääritelmään: satunnainen yksilö, eniten pisteytetty yksilö, nopein yksilö ja tehokkain yksilö.

Kuva 3.

Vertaa suorituskykyä pistemäärän (A), nopeuden (B) ja tehokkuuden (C) suhteen vuorovaikutuksessa olevien ryhmien ja nimellisten ryhmien välillä. Tiedot yhdistetään kaikissa kuudessa lohkossa ja standardoidaan (eli muunnetaan z-pisteiksi) kullakin tehtävän monimutkaisuustasolla (erot ovat suhteellisia monimutkaisuustason sisällä, eikä niitä pidä verrata monimutkaisuustasojen välillä). Virhepalkit osoittavat 95 %:n luottamusvälit. Olemme toistaneet tässä kuvassa esitetyt analyysit kullekin lohkolle laadullisesti samanlaisin tuloksin (SI Liite, osa S3 ja kuvat S8–S10).

Suorituskyky ratkaisun laatuna.

Kaikilla tehtävän monimutkaisuuden tasoilla kuva 3A osoittaa, että ryhmät saavat korkeammat pisteet kuin satunnaisesti valitut, nopeimmat ja tehokkaimmat jäsenet vastaavan kokoisista nimellisryhmistä ( P = 0,013, 95 % CI [0,026, 0,225]; P < 0,001, 95 % CI [0,184, 0,410]; P < 0,001, 95 % CI [0,155, 0,378], mutta pienempi kuin korkein) jäsen (P = 0,047, 95 % CI [-0,159, -0,001]; katso SI-liite, taulukot S4–S7, regressiotaulukot). Tämä tulos on yhdenmukainen pitkäaikaisten havaintojen kanssa (33⇓⇓⇓–37), että vuorovaikutuksessa olevat ryhmät ovat usein parempia kuin nimelliset ryhmät ratkaisun laadussa, kun standardi asetetaan keskimääräisen jäsenen kriteerillä (heikko synergia), mutta ei silloin, kun sen asettaa paras jäsen -kriteeri (vahva synergia).

Suorituskyky nopeudena.

Kuva. Kuva 3B osoittaa, että vuorovaikutuksessa olevat ryhmät suorittavat monimutkaisempia tehtäviä - mutta eivät yksinkertaisempia - nopeammin kuin vastaavan kokoisten nimellisten ryhmien satunnaiset ja eniten pisteet saaneet jäsenet. Lisäksi vuorovaikutuksessa olevat ryhmät ovat yhtä nopeita kuin nopeimmat ja tehokkaimmat jäsenet korkeimmassa tehtävän monimutkaisuudessa (katso SI-liite, taulukot S8–S10, regressiotaulukot). Nämä viittaavat siihen, että tehtävissä, joissa on monia komponentteja (opiskelijat ja huoneet) ja tiheitä keskinäisiä riippuvuuksia (monia rajoituksia), työn jakamisesta ryhmälle saatavat hyödyt voivat olla suuremmat kuin vuorovaikutuksessa oleviin ryhmiin liittyvät prosessihäviöt, mikä on yhdenmukaista aiemman työn havaintojen kanssa ( 36).

Suorituskyky tehokkuutena.

Lopuksi kuva 3C osoittaa, että monimutkaisimmissa tehtävissä nopeuden lisäys ylittää pistemäärän alijäämät. Tämä johtaa silmiinpistävään vuorovaikutukseen tehtävän monimutkaisuuden ja työn järjestelyn välillä: vaikka vuorovaikutuksessa olevat ryhmät ovat huomattavasti vähemmän tehokkaita kuin nimellisten ryhmien valitut jäsenet yksinkertaisissa tehtävissä, niiden suhteellinen tehokkuus kasvaa tehtävän monimutkaisuuden myötä, kunnes ne ylittävät korkeimman pistemäärän, nopeimman ja tehokkaimman. monimutkaisia jäseniä (katso SI-liite, taulukot S11–S13, regressiotaulukot). Tämä tulos muistuttaa ryhmäpäätöksentekoa sosiaalisten hyönteisten keskuudessa, jossa tuoreessa tutkimuksessa on havaittu, että muurahaisyhdyskunnat ovat parempia kuin yksittäiset muurahaiset, kun syrjintätehtävä on vaikea, mutta ei silloin, kun se on helppoa (38).

Ryhmäsynergian purkaminen.

Havainto, että vuorovaikutuksessa olevat ryhmät ovat tehokkaampia kuin vastaavan kokoisten nimellisten ryhmien parhaiten valitut jäsenet – millä tahansa neljästä määritelmästämme – kun tehtävä on monimutkainen, mutta ei silloin, kun tehtävä on yksinkertainen, viittaa siihen, että prosessihäviöiden ja synergististen hyötyjen välinen tasapaino riippuu tehtävän monimutkaisuudesta. Tämän riippuvuuden ymmärtämiseksi paremmin ja huomioimalla, että (kuva 2C) näkyvä tehokkuuden vaihtelu riippuu enemmän tehtävän keston vaihtelusta (joka vaihtelee keskimäärin 2 ja 6 minuutin välillä, kuva 2B) kuin saavutetun pistemäärän vaihtelusta. (joka vaihtelee keskimäärin 95 % ja 85 % välillä, kuva 2A), esitämme seuraavaksi tutkivan analyysin tehtävän kussakin vaiheessa käytetystä ajasta. Tämä analyysi on mahdollista tietojemme erittäin yksityiskohtaisen luonteen ansiosta. Koska jokaisen osallistujan jokainen toimenpide on aikaleimattu, voimme jakaa kokonaisratkaisun ajan erittäin tarkasti mitattuihin segmentteihin, jotka vastaavat ongelmanratkaisuprosessin eri vaiheita. Selvyyden vuoksi määrittelemme neljä avainsegmenttiä, jotka on esitetty kaavamaisesti kuvassa 4A:

Kuva 4.

Tehtävän suorittamisen virstanpylväät. (A) Ongelmanratkaisuprosessin neljä virstanpylvästä: (i) ensimmäinen väliratkaisu luodaan, (ii) paras väliratkaisu luodaan, (iii) lopullinen ratkaisu luodaan ja (iv) lopullinen ratkaisu lähetetty. (B, D, F ja H) Ryhmien ja yksilöiden käyttämä aika (minuutteina) (joko satunnainen, eniten pisteytetty, nopein tai tehokkain) kussakin aikajaksossa. (C, E, G ja I) Standardoitu käytetty aika (muunnettu z-pisteisiin; ts. osoittaa suhteellista eroa kompleksisuustason sisällä) kussakin aikasegmentissä. Virhepalkit osoittavat 95 %:n luottamusvälit.

Aika ensimmäiseen ratkaisuun, $T1$ .

Tehtävän alusta ensimmäisen ratkaisun luomiseen kuluvaa aikaa voidaan pitää strategian muotoiluun käytettynä aikana lähestyä tehtävää.

Parhaan ratkaisun aika, $T2$ .

Paras ratkaisu ei välttämättä ole lähetetty, koska tehtäväinstanssi päättyy vasta, kun ryhmä/yksilö päättää lähettää ratkaisu, ja ryhmät/yksilöt voivat luoda ratkaisuja parhaan ratkaisunsa jälkeen palaamatta siihen.

Aika parhaasta lopulliseen ratkaisuun, $T3$ .

Parhaiden ja lopullisten ratkaisujen luomisen välillä kuluva aika, jota voidaan pitää "ylimääräisenä tutkimisena". heikentää tehokkuutta, koska se johtaa huonompaan (tai samaan) ratkaisun laatuun, mutta pidentää tehtävän kokonaiskestoa.

Aika lopullisesta ratkaisusta lähettämiseen, $T4$ .

Lopullisen ratkaisun luomisen ja sen lähettämisen välillä kuluva aika, joka voidaan katsoa " sitoutumisaika”, voi olla toinen tehottomuuden lähde, koska se johtaa tasaiseen ratkaisun laatuun, mutta pidentää tehtävän kokonaiskestoa.

Kuva Kuva 4 esittää kaksi vertailusarjaa vuorovaikutteisten ja nimellisten ryhmien välillä kullekin näistä neljästä segmentistä. Kuvat 4 B, D, F ja H näyttävät raakakestot kohteille $T1$ , $T2$ , $T3$ ja $T4$ math>, vastaavasti vuorovaikutuksessa oleville ryhmille (vihreä) yhdessä neljän aiemmin määritellyn nimellisen ryhmän vertailuarvon kanssa (satunnainen jäsen, eniten pisteitä saava jäsen, nopein jäsen ja tehokkain jäsen), kun taas kuva 4 C, E, G ja I näyttää samat tulokset kuin standardoidut kestoajat. Teemme viisi päähavaintoa kuvasta 4.

Ensinnäkin havaitsemme, että (keskimäärin) vuorovaikutuksessa olevat ryhmät viettävät vähemmän aikaa $T1:ssä$ (aika ensimmäiseen ratkaisuun, kuva 4 B ja C) kuin nimellisten ryhmien jäsenet tehtävän monimutkaisuudesta riippumatta ( $P<0,001$ kaikille ja SI-liite, taulukko S14). Arvelemme, että tämä havainto voi liittyä viimeaikaisten tutkimusten väitteisiin, joiden mukaan ryhmään kuuluminen vähentää vastuuntuntoa ja katumusta, joita jäsenet voivat kohdata samoissa olosuhteissa yksilöllisesti. Jos se on oikein, heikentynyt emotionaalinen este toiminnalle voi olla taustalla oleva mekanismi, joka saa ryhmän jäseniä toimimaan aikaisemmin (39).

Toiseksi havaitsemme tehtävän monimutkaisuuden huomattavan vaikutuksen $T2:een$ (aika parhaaseen ratkaisuun, kuva 4 D ja E): vuorovaikutuksessa olevat ryhmät saavuttavat parhaan ratkaisunsa hitaammin kuin nopeimmat. ja nimellisten ryhmien tehokkaimmat jäsenet vähiten monimutkaisessa tehtävässä, mutta nopeammin kaikkein monimutkaisimmassa tehtävässä (P < 0,001, 95 % CI:t [0,119, 0,385] ja [0,109, 0,371], vastaavasti, pienimmässä monimutkaisessa tehtävässä, ja P < 0,001, 95 % CI:t [-0,351, -0,085] ja [-0,370, -0,108], tässä järjestyksessä, suurimmalla monimutkaisuudella; katso regressiotaulukot SI-liitteen taulukoista S17–S18). Tärkeää on, että suurin osa tehtävän kestosta kuluu tässä segmentissä, mikä viittaa siihen, että nopeus parhaaseen ratkaisuun on tärkein tekijä ryhmäsynergiassa. Yksi mahdollinen selitys sille, miksi vuorovaikutuksessa olevat ryhmät ovat nopeampia löytämään parhaan ratkaisun erittäin monimutkaisessa tilanteessa, on se, että vuorovaikutuksessa olevat ryhmät ymmärtävät joitain työnjaon etuja (katso SI-liite, osa S4 ja kuva S11, vihjailevia todisteita varten). Toinen mahdollinen selitys, jolle näemme chat-lokeissa joitakin anekdoottisia todisteita (SI-liite, kuva S11), on se, että vuorovaikutuksessa olevat ryhmät ovat halukkaampia tyydyttämään hyväksymällä tällä hetkellä saatavilla olevan ratkaisun tyydyttäväksi (40). Vielä toinen voisi olla, että he hyötyvät vuorottelusta, jossa yksi henkilö on ensisijaisesti aktiivinen, kun taas muut harkitsevat seuraavaa siirtoaan. Valitettavasti nykyinen kokeilusuunnitelma ei salli meidän tehdä eroa näiden vaihtoehtoisten selitysten välillä, joten ne jäävät spekulatiivisiksi.

Kolmanneksi havaitsemme, että monimutkaisuudesta riippumatta vuorovaikutuksessa olevat ryhmät viettävät enemmän aikaa $T3$ -segmentissä (ylimääräinen etsintä, kuva 4 F ja G) suhteessa nimellisten ryhmien jäseniin; Kuten $T1$ :ssa, ero on johdonmukainen monimutkaisuustasojen välillä (katso SI-liite ja taulukot S19–S20 regressiotaulukot). Neljänneksi, vuorovaikutuksessa olevat ryhmät käyttävät myös enemmän aikaa sitoutumiseen ratkaisuun ( $T4$ ) kuin nimellisten ryhmien valitut jäsenet, jälleen kerran monimutkaisuudesta riippumatta (Kuva 4 H ja I ja SI-liite, taulukko S14) . Arvelemme, että se tosiasia, että vuorovaikutuksessa olevat ryhmät voivat kommunikoida chatin kautta (ja heiltä puuttuu määrätty johtaja), voi lisätä ryhmille painetta varmistaa, että heidän päätöksensä tehdään kollektiivisesti (eli konsensuksen saavuttaminen), mikä voi myötävaikuttaa havaittuun vaikutukseen.

Viidenneksi, havaitsemme, että tehtävän keskimääräinen kokonaiskesto vaihtelee $∼2$ minuutista erittäin alhaisen monimutkaisuuden tapauksessa $∼6$ minuuttiin erittäin monimutkaisessa tapauksessa (maksimimäärästä 10 min), mikä tarkoittaa, että osallistujat lähettävät yleensä ratkaisun ja lopettavat tehtävän ennen kuin aika loppuu. Tämä havainto on merkityksellinen analyysimme kannalta, koska aikarajoitukset eivät vaikuta vuorovaikutuksessa olevien ryhmien suorituskykyvertailuihin nimellisten ryhmien valittujen jäsenten suorituskykyyn.

Yhteenvetona voidaan todeta, että kuva 4 paljastaa kahden tyyppisiä prosessihäviöitä (eli ylimääräiseen etsintään ja yhteisymmärrykseen pääsemiseen käytetty aika) ja kahden tyyppisiä synergiaetuja (eli nopeampi aika ensimmäiseen ratkaisuun ja nopeampi paras ratkaisu monimutkaisissa tehtävissä ). Mielenkiintoista on, että kun synergiaetu – erityisesti parhaan ratkaisun saavuttamiseen kuluvassa ajassa – riippuu tehtävän monimutkaisuudesta, prosessihäviöt eivät. Toisin sanoen havaintomme viittaavat siihen, että vuorovaikutteisessa ryhmässä olemisella on kiinteät kustannukset, jotka ovat suhteellisen yhdenmukaisia tehtävien monimutkaisuustasoilla, mutta hyöty, joka vaihtelee monimutkaisuustasojen välillä (eli vähemmän aikaa parhaan ratkaisun löytämiseen).

Tämän havainnon selventämiseksi lisäämme seuraavaksi kustannukset ja hyödyt, jotta voidaan kvantifioida tehtävän suorittamisen arvo vuorovaikutteisessa ryhmässä monimutkaisuustasoilla. Erityisesti mittaamme kutakin kustannusta ja hyötyä vuorovaikutuksessa olevien ryhmien ja kunkin aikasegmentin nimellisten ryhmien satunnaisen (eli keskimääräisen) jäsenen absoluuttisena erona käytettynä aikana: $Kokonaishyöty=T1nominal−T1vuorovaikutus+ T2nominal−T2interactingKokonaiskustannukset =T3vuorovaikutus−T3nimellinen+T4vuorovaikutus−T4nimellinen.$

Kuva Kuva 5 osoittaa, että vuorovaikutteisten ryhmien tehottomuuteen (eli ylimääräiseen etsintään, konsensuksen saavuttamiseen) liittyvät kokonaiskustannukset ylittävät synergistiset hyödyt (eli nopeushyödykkeet parhaan ratkaisun löytämisessä) kun ratkaistaan vähän monimutkaisia tehtäviä, mutta eivät erittäin monimutkaisia tehtäviä. Tämä selittää havaintomme, jonka mukaan ryhmät ovat tehokkaampia kuin vastaavankokoisten nimellisten ryhmien korkeimmat, nopeimmat ja tehokkaimmat jäsenet, kun tehtävä on monimutkainen, mutta tämä suhde on päinvastainen, kun tehtävä on yksinkertainen. Löydämme samanlaisia tuloksia eniten pisteitä saaneesta jäsenvertailusta (SI-liite, osa S5 ja kuva S12).

Kuva 5.

Vuorovaikutteisten ryhmien kustannus-hyöty. Kuvassa on esitetty absoluuttinen ero keskimääräisessä vuorovaikutuksessa olevien ryhmien ja keskimääräisen yksittäisen nimellisen ryhmän välillä kussakin aikasegmentissä.

Tutkimme eroja ongelmanratkaisumenetelmissä.

Tärkeimmät tulokset voidaan todeta, että vuorovaikutuksessa olevat ryhmät ovat tehokkaampia kuin nimellisten ryhmien tehokkain jäsen monimutkaisissa ongelmissa. Tästä syystä päättelemme, että niillä on vahva tehokkuussynergia (kuva 3C). Nopeuden suhteen vuorovaikutuksessa olevat ryhmät ovat nopeampia kuin keskimääräinen (satunnaisesti valittu) jäsen ja yhtä nopeita kuin vastaavankokoisten nimellisten ryhmien nopein jäsen (kuvio 3B), jolloin niillä on vain heikko synergia. Ratkaisun laadun kannalta vuorovaikutuksessa olevat ryhmät osoittavat vielä heikompaa synergiaa, koska ne saavat korkeammat pisteet kuin keskimääräinen jäsen, mutta eivät aivan yhtä hyvin nimellisten ryhmien eniten pisteyttänyt jäsen (kuva 3A).

Näiden tulosten tutkimiseksi lähemmin tarkastelimme luotujen väliratkaisujen määrää ja vauhtia, jossa väliratkaisu määritellään opiskelijoiden jakamiseksi huoneisiin (eli jokainen osallistujan tekemä toimenpide tuottaa väliratkaisun). Kuten kuvista 6 A ja B on esitetty, havaitsemme, että ryhmät eivät vain tuottaneet enemmän väliratkaisuja kuin satunnaiset, korkeimman pistemäärän saaneet, nopeimmat ja tehokkaimmat jäsenet vastaavan kokoisissa nimellisryhmissä ( $P<0,001$ ). kaikille, 95 % luottamusvälit $[0.503;0.697]$ , $[0.586;0.738]$ , $[0.513;0.736]$ ja $[ 0,544,0,745]$ ; SI-liite, taulukko S23); he tekivät niin myös korkeammalla tahdilla ( $P<0,001$ kaikille, 95 % CI:t $[0,424,0,662]$ , $[0,615,0,815]$ , $[0,104,0,372]$ ja $[0,127,0,392]$ ; SI-liite, taulukko S23). Vuorovaikutuksessa olevilla ryhmillä oli myös laajempi ratkaisusäde, joka määriteltiin suurimmaksi muokkausetäisyydeksi (eli opiskelija-/huonetehtävien erojen lukumääräksi) ensimmäisen täydellisen ratkaisun (eli kaikki opiskelijat, jotka on määrätty huoneisiin, mutta ristiriidat saattavat jäädä ratkaisematta) ja kaikkien myöhempien ratkaisujen välillä. täydellisiä ratkaisuja, mikä viittaa siihen, että he tutkivat ratkaisuavaruutta laajemmin (kuva 6C; $P<0,001$ kaikille, 95 % CI:t $[0,558,0,772]$ , $[0,582 ,0,802]$ , $[0,597,0,797]$ ja $[0,600,0,800]$ ; SI-liite, taulukko S23). Vahvistimme myös tämän laadullisen päätelmän kahdella muulla etsintämittauksella: niiden ratkaisujen prosenttiosuus, jotka ovat muokkausetäisyydellä kahdesta lopullisesta ratkaisusta, ja niiden väliratkaisujen prosenttiosuus, joihin liittyi rajoitteen rikkominen (SI-liite, kuvat S13 ja S14).

Kuva 6.

Mekanistiset erot ongelmanratkaisumenetelmissä vuorovaikutuksessa olevien ryhmien ja yksilöiden välillä. Vuorovaikutteiset ryhmät luovat (A) enemmän ratkaisuja, (B) nopeammin ja (C) tutkivat ratkaisuavaruutta laajemmin. (D) Parhaiten löydetyn ratkaisun laatu ei kuitenkaan ole parempi kuin eniten pisteitä saaneiden yksittäisten nimellisten ryhmien ratkaisu. Virhepalkit osoittavat 95 %:n luottamusvälit.

Näiden havaintojen valossa on sitäkin yllättävämpää, että vuorovaikutuksessa olevat ryhmät eivät löytäneet laadukkaampia ratkaisuja kuin nimellisryhmien eniten pisteyttänyt jäsen (kuva 6D; $P=0,268$ ; SI-liite, taulukko S23). Osittain ero voidaan selittää sillä, että vuorovaikutuksessa olevat ryhmät eivät myöskään ole toimittaneet parasta löydettyä ratkaisuaan nopeammin kuin eniten pisteitä saaneet henkilöt: kaikista monimutkaisimmista pisteistä eniten pisteitä saanut henkilö ei lähetä parasta löydettyä ratkaisuaan $~6 %$ ajasta, kun taas vuorovaikutuksessa olevat ryhmät eivät toimita parhaita ratkaisujaan $∼14 %$ ajasta ( $P<0,001$ ; ero suhteissa). Tämän seurauksena vuorovaikutteisten ryhmien lähettämät ratkaisut olivat huonompia suhteessa korkeimman pistemäärän saaneisiin yksittäisiin jäseniin kuin jos kaikki olisivat lähettäneet parhaan löytämänsä ratkaisun (vertaa kuvaa 3A kuvaan 6D), vaikka silloinkin jää jäljelle.

Mistä voi johtua vahvan tehokkuuden synergia ja ratkaisun laadun ja nopeuden vain heikko synergia? Aiempi tutkimus, jossa ongelmanratkaisu on käsitteellistää adaptiivinen haku karussa suoritusmaisemassa (14, 27), jossa jokainen piste maisemassa edustaa yhtä ratkaisua huonetehtävään ja pisteen korkeus edustaa kyseisen tehtävän suorittamista, tarjoaa useita, mahdollisesti toisiinsa liittyviä selityksiä. Yksi mahdollinen selitys on, että eniten pisteitä saaneilla henkilöillä on paremmat esitykset (alemman ulottuvuuden likiarvot) todellisesta suorituskyvystä, minkä ansiosta he voivat arvioida ratkaisuja (ja ratkaisureittejä) offline-tilassa testaamatta niitä kokeilujen avulla (41, 42). Paremmat esitykset voivat johtaa tarkempiin offline-arviointeihin ja tehokkaampiin hakutoimiin (26, 43, 44), joille on ominaista vähemmän väliratkaisuja ja korkeampi ratkaisujen laatu. Vaihtoehtoisesti ongelmanratkaisijoiden ryhmillä voi olla ristiriitaisia etuja (esim. pisteiden maksimointi vs. keston minimoiminen) ja siten erilaisia näkemyksiä oikeasta toimintatavasta (45). Jos tämä on totta, ryhmät voivat hyötyä keskitetystä koordinoinnista nimeämällä ryhmän johtaja (45) tai prosessiin liittyvistä interventioista, kuten vuorovaikutuksen ajoittaisten taukojen pakottaminen (46, 47). Vielä yksi mahdollisuus on, että kun aika on rajallinen, hakustrategiat, jotka mahdollistavat nopeat voitot (eli jyrkät suorituskyvyn parannukset varhaisessa vaiheessa) ja vähentävät tutkimisen määrää, saattavat näyttää ylivoimaisilta (26). Näin ollen vaikka paikallinen polkua syventävä hakustrategia (esim. mäkikiipeily), jonka vastaavan kokoisten nimellisten ryhmien eniten pisteet saaneet jäsenet omaksuvat, saattaa tarjota lyhyen aikavälin suorituskykyetuja, vuorovaikutteisten ryhmien strategia hakualueen laajentamiseksi saattaa olla edullisempi. pitkällä aikavälillä (48, 49).

Keskustelu

Monissa kiinnostavissa tehtävissä johtajat voivat päättää, antaako tehtävän vuorovaikutuksessa olevalle ryhmälle vai vastaavalle määrälle itsenäisesti työskenteleviä henkilöitä (12). Tällaisten asetusten osalta tulokset tarjoavat useita oivalluksia. Ensinnäkin päätösten työn jakamisesta – vuorovaikutuksessa oleville ryhmille tai nimellisille ryhmille – pitäisi riippua käsillä olevan tehtävän monimutkaisuudesta ja suorituskyvyn arvioinnista. Jos esimies haluaa esimerkiksi löytää toimivan ratkaisun CSOP:hen mahdollisimman lyhyessä ajassa, suositus olisi pyytää ryhmää ratkaisemaan ongelma, kun ongelma on monimutkainen, mutta kysyä riippumattomia ongelmanratkaisijoita, kun se on yksinkertainen. On huomionarvoista, että tässä esitetyt kesto- ja tehokkuustulokset saattavat itse asiassa aliarvioida kuinka tämä toimisi käytännössä. Jos työ esimerkiksi järjestettäisiin nimellisryhmissä, järjestely tuottaisi silti useita erilaisia ratkaisuja, joiden välillä joku johtaja voi päättää. Vaikka nimellisryhmien operaatiomme simuloi tilannetta, jossa johtaja tekee päätöksen välittömästi, on tilanteita, joissa esimies saattaa haluta pohtia eri ratkaisujen etuja, ja tämä veisi nollasta poikkeavaa aikaa. Näin ei ole vuorovaikutuksessa olevissa ryhmissä, joissa päätöksentekoprosessi sisältyy jo ongelmanratkaisuharjoituksen kuluneeseen aikaan.

Toiseksi havainnot viittaavat myös siihen, että mahdollinen selitys sille, miksi ryhmäprosessien häviöt ovat olleet näkyvämmin esillä tutkimustuloksissa kuin synergistiset hyödyt (12), on se, että ryhmän suorituskyvyn laboratoriotutkimukset perustuvat yleensä hyvin yksinkertaisiin tehtäviin. Todellakin, tähän mennessä selkein laboratoriotodistus ylivoimaisesta ryhmän suorituskyvystä, vaikkakin harvinaista, tulee ryhmiltä, jotka työskentelevät suhteellisen monimutkaisten tehtävien parissa (13, 46, 50, 51); Kuitenkin se tosiasia, että tehtävän monimutkaisuutta ei vaihdettu systemaattisesti yhdessä tutkimuksessa, on pääasiallinen hallitsemattoman vaihtelun lähde aikaisemmissa tutkimuksissa (17, 36).

Kolmanneksi analyysimme siitä, kuinka vuorovaikutuksessa olevat ryhmät ja itsenäiset yksilöt eroavat toisistaan ongelmanratkaisuprosessin eri osissa viettämänsä ajan suhteen, tarjoaa käsityksen siitä, kuinka ryhmäprosesseja voitaisiin parantaa. Esimerkiksi havaintomme, jonka mukaan ryhmät käyttävät enemmän aikaa päättäessään, että tehtävä on suoritettu (eli konsensuksen saavuttaminen), viittaa siihen, että jos ryhmän johtajalle määrätään yksipuolinen kyky tehdä tämä päätös, kuten yksilö tekee, pitäisi vähentää tätä viivettä. , mikä parantaa ryhmän suorituskykyä. Lisäksi havaintomme, jonka mukaan vuorovaikutuksessa olevat ryhmät eivät todennäköisesti toimita parasta ratkaisuaan, viittaa siihen, että parhaiden ratkaisujen tallentaminen siten, että ne voidaan ladata uudelleen ja mahdollisesti muokata myöhemmissä vaiheissa (henkilökohtaisen tuottavuusohjelmiston kaikkialla esiintyvä ominaisuus), pitäisi myös parantaa niiden suorituskykyä ( 46).

Neljänneksi, analyysimme ryhmien ja yksilöiden ratkaisudynamiikasta herättää lisäarvoituksia tulevaa työtä varten. Erityisesti, jos ryhmät luovat enemmän ratkaisuja nopeammin ja tehokkaammin laajemmalla ratkaisualueella kuin jopa eniten pisteitä saaneet yksilöt, miksi he eivät löydä parempia ratkaisuja?

Lopuksi päättelemme, että ryhmäsuorituskykyä koskeva tiede hyötyisi syvemmästä, järjestelmällisemmästä ymmärtämisestä niiden tehtävien yhtäläisyyksistä ja eroista, joita ryhmiä pyydetään suorittamaan sekä laboratoriossa että kentällä. Tarvitaan kattava, empiirisesti perusteltu teoria ryhmätehtävistä (12). Tutkimusohjelma, joka vaihteli systemaattisesti tehtävätyyppejä sekä sallittuja ryhmäprosesseja ja muita kontekstuaalisia tekijöitä, edistäisi ryhmäongelmanratkaisun perustieteitä samalla kun se käsittelee käytännön sovelluksia.

Materiaalit ja menetelmät

Tutkimuksen arvioi Microsoft Research Ethics Advisory Board, ja sen hyväksyi Microsoft Research Institutional Review Board (MSR IRB; Approval 0000019). Kaikki osallistujat antoivat nimenomaisen suostumuksen osallistua tähän tutkimukseen, ja MSR IRB hyväksyi suostumusmenettelyn. Kokeellinen suunnittelumme, otoskokomme ja analyysimme, joissa verrattiin vuorovaikutuksessa olevien ryhmien ja nimellisten ryhmien suorituskykyä, rekisteröitiin etukäteen ennen tietojen keräämistä (AsPredicted 13123). Kaikki muut analyysit ovat tutkivia.

Algoritminen Ratkaisija.

Mallinnoimme jokaisen huonetehtävätehtävän sekakokonaislukuohjelmointitehtävänä ja loimme tietokoneille suoritusajan kunkin ongelman ratkaisemiseen käyttämällä IBM ILOG CPLEX Optimization Studio -ohjelmistoa, joka on korkean suorituskyvyn matemaattinen ohjelmointiratkaisin lineaariseen ohjelmointiin, sekakokonaislukuohjelmointiin ja toisen asteen ohjelmointiin. Ohjelmisto toimi kannettavassa tietokoneessa, jossa oli Intel Core i5 -mikroprosessori, joka toimi 2,6 GHz:n nopeudella. Suoritimme ohjelmiston parametrien oletuskonfiguraatiolla. Tehtävätiedoston suoritusajan yksikkö on "tiks", joka on CPLEXin yksikkö tehdyn työn määrän mittaamiseksi. Tikkien vastaavuus kellonaikaan vaihtelee alustoittain (mukaan lukien laitteisto, ohjelmisto, koneen kuormitus jne.), mutta kun otetaan huomioon sekakokonaislukuohjelmointiongelma ja parametriasetukset, ongelman ratkaisemiseen tarvittavat tikit ovat deterministisiä. Tässä mielessä algoritmisen ratkaisijan testi-uudelleentestausluotettavuus on 1. Katso lisätietoja SI-liitteen kohdasta 1.4.2.

Tilastollinen analyysi.

Koska jokainen vuorovaikutuksessa oleva ryhmä (tai yksilö) suoritti viisi huonetehtävää, teimme testejä olosuhteiden välisistä eroista tehtävätasolla. Vuorovaikutusvaikutuksia varten mallisimme tiedot käyttämällä yleistettyä lineaarista sekamallia kullekin tulokselle (esim. pisteet, kesto ja tehokkuus) satunnaisella vaikutuksella ryhmälle tai yksittäiselle tunnisteelle. Nämä mallit ottavat huomioon tietojen sisäkkäisen rakenteen. Kaikki tilastolliset testit olivat kaksisuuntaisia (esirekisteröinnin mukaan). Tilastollisten testien yksityiskohdat ovat SI-liitteen kohdassa S7.

Standardoidut kertoimet.

Mahdollistaaksemme tehosteiden kokojen merkityksellisen vertailun eri monimutkaisuustasoisten tehtävien välillä standardoimme erilaisia suorituskykymittareita (esim. pisteet, kesto, tehokkuus ja ratkaisujen määrä). jokaisella monimutkaisuustasolla. Esimerkiksi mittauksen X standardoitu arvo, joka on mitattu tehtäväinstanssille i, jonka monimutkaisuus on c, määritellään seuraavasti: $Xi,standardized=Xi−μX,cσX,c,$ jossa $μX,c määritellään X:n keskiarvona kaikissa tehtävän esiintymisissä kompleksisuudessa c (vuorovaikutteisille ja nimellisille ryhmille), ja σX,c on SD.$

Tietojen saatavuus

Replikaatiotiedot ja koodi ovat saatavilla Harvard Dataverse:ssä, https://doi.org/10.7910/DVN/RP2OCY (52). Kokeilu kehitettiin Empirica-alustalla (53). Huonetehtävän lähdekoodi löytyy osoitteesta https://github.com/amaatouq/room-assignment-csop ja Reading the Mind in the Eyes -testin lähdekoodi osoitteesta https://github .com/amaatouq/rme-test.

Kiitokset

Kiitämme Valery Yakubovichia, Hazhir Rahmandadia ja James Houghtonia hyödyllisistä keskusteluista ja palautteesta. Kirjoittajat kiittävät Alfred P. Sloan Foundation (G-2020-13924) taloudellisesta tuesta.

Alaviitteet

Kirjoittajat: A.A., M.Y. ja D.J.W. suunniteltu tutkimus; A.A., M.Y. ja D.J.W. suoritettu tutkimus; A.A., M.A., M.Y. ja D.J.W. mukana uusia reagensseja/analyyttisiä työkaluja; A.A., M.A., M.Y. ja D.J.W. analysoidut tiedot; ja A.A., M.A., M.Y. ja D.J.W. kirjoitti lehteen.

Kirjoittajat eivät ilmoittaneet kilpailevia etuja.

Tämä artikkeli on suora PNAS-lähetys.

Tämä artikkeli sisältää tukitietoja verkossa osoitteessa https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2101062118/-/DCSupplemental.

Tämä avoimen pääsyn artikkeli on jaettu Creative Commons Attribution-NonCommercial-NoDerivatives -lisenssin 4.0 (CC BY-NC-ND) alla.