Le preguntamos al cosmólogo Pau Figueras todo lo que siempre quisiste saber sobre los agujeros negros. En la otra parte de la entrevista explicó qué son los agujeros negros, físicamente, y cómo esperamos observarlos. En esta segunda parte de la entrevista, explica cómo las teorías de Einstein predicen su existencia y cómo describirlas matemáticamente.
Tenga en cuenta que desde que se realizó esta entrevista, se han detectado pruebas contundentes de agujeros negros. Proviene de ondas gravitacionales. ¡Vea que los agujeros negros existen! Para descubrir mas.
¿Cómo se predijeron por primera vez los agujeros negros?
Einstein publicó su [teoría general de la relatividad] a finales de 1915,
y solo unos meses después, a principios de 1916, [Karl]
Schwarzschild encontró la primera solución de las ecuaciones de Einstein. [Por solución nos referimos a algunos valores para las variables que describen la curvatura del espacio-tiempo y la distribución de la materia que satisfacen las ecuaciones de Einstein].
[Esta solución] describe el campo gravitacional de un cuerpo de simetría esférica: un agujero negro.
En ese momento no se entendía que esa solución correspondiera a una
calabozo. De hecho, incluso en los años 30, las mentes más brillantes de esa época,
[incluido] el propio Einstein, despreciaba la idea de un agujero negro
porque contenía una singularidad, a saber, un lugar donde la curvatura es
tan grande que incluso la relatividad general se derrumba. Se necesitaron casi 50
años para comprender realmente qué es un agujero negro, y esto solo se hizo en la década de 1960.
La relatividad general afirma que los objetos masivos curvan el espacio-tiempo. ¿Cómo afectan los agujeros negros a la curvatura del espacio-tiempo?
La fuerza del campo gravitacional se mide en términos de curvatura. Y debido a que los agujeros negros son muy masivos y muy pequeños, su gravedad es muy fuerte y [crea] una curvatura muy grande del espacio-tiempo.
Una forma de caracterizar la curvatura es algo llamado radio de Schwarzschild :
donde $ G_ N $ es la constante [de gravedad] de Newton, $ M $ es la masa del objeto y $ c $ es la velocidad de la luz.
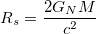
El radio de Schwarzschild es, más o menos, el tamaño que debería tener un objeto dado, con una masa determinada, para que sea un agujero negro. Por ejemplo, si logramos concentrar toda la masa de la Tierra en una esfera de un radio de unos pocos centímetros, entonces ese objeto sería un agujero negro.
Por supuesto, sabemos que esto no puede suceder porque hay otras fuerzas en la naturaleza que lo impiden, pero en otras circunstancias puede suceder. Por ejemplo, cuando las estrellas muy masivas se quedan sin combustible nuclear, se enfrían y colapsan, y en algún momento se vuelven lo suficientemente pequeñas como para que toda la masa encaje dentro de un radio de Schwarzschild ; por lo tanto, forman un agujero negro.
Por ejemplo, el radio de Schwarzschild del Sol es del orden de unos pocos kilómetros. Entonces, si logramos concentrar toda la masa del Sol en una esfera de unos pocos kilómetros, entonces sería un agujero negro.
<p style="text-align:left">¿Puede caracterizar un agujero negro de manera tan simple, con solo algunas características, como la masa y el tamaño?
Una de las razones por las que los agujeros negros son tan importantes en nuestra comprensión de la relatividad general es por su simplicidad , porque están hechos de los bloques de construcción más fundamentales de la teoría, a saber, el espacio y el tiempo únicamente. Son muy simples y por tanto podemos entenderlos.
Esto [está en contraste con] otros objetos gravitacionales, como las estrellas. Para comprender una estrella, [además de necesitar] tener en cuenta la relatividad general, también es necesario comprender la física nuclear para tener en cuenta las reacciones nucleares [y] la física del plasma para comprender el transporte de calor dentro de la estrella. Esto se vuelve muy complicado y a menudo nos vemos llevados a estudiar estos objetos dentro de ciertas aproximaciones.
No tenemos que hacer eso con los agujeros negros porque solo están hechos de espacio y tiempo, por lo que tenemos una comprensión completa de ellos solo dentro de nuestra teoría. No necesitamos ninguna otra física. Esta simplicidad se traduce en el hecho de que solo se describen en términos de muy pocos parámetros.
En el caso del vacío, si el agujero negro es estático, entonces debe ser esférico y solo hay un parámetro que caracteriza al agujero negro, a saber, su masa. [Sin embargo], los objetos en la naturaleza, como las estrellas, giran, por lo que los agujeros negros que ocurren en la naturaleza deberían tener cierta rotación. La solución de Schwarzschild se encontró [apenas] meses después de que Einstein publicara su teoría, pero tomó otros 50 años encontrar la solución general que tiene rotación y es relevante para describir los agujeros negros [que podríamos encontrar en] la naturaleza. Esta solución de Kerr se describe en su totalidad por solo dos parámetros, a saber, la masa y el giro del agujero negro. Con estos dos parámetros puede caracterizar completamente todos los agujeros negros en la naturaleza y no necesitamos hacer ninguna aproximación para comprender esos objetos. Por eso son tan importantes.
En cierto sentido, los agujeros negros no son diferentes de las partículas elementales [en física de partículas] porque solo necesitamos especificar unos pocos parámetros [para describirlos]. Lo mismo ocurre con los agujeros negros: [ellos] son las partículas elementales de la relatividad general.
¿Son los agujeros negros el mayor misterio abierto de la relatividad general?
Si. Los agujeros negros son una predicción de la relatividad general y conocemos varios casos en la naturaleza en los que pensamos que deberían ocurrir, pero aún no los hemos detectado. Así que todavía es una pregunta abierta si [existen] o no, o si tienen las propiedades que predice la relatividad general.
Esto es importante porque la mayoría de las pruebas [de] relatividad general [involucran] situaciones en las que la gravedad es débil o relativamente débil. Por ejemplo, hemos probado la curvatura de la luz, la precesión del perihelio de Mercurio.
La detección de agujeros negros sería importante porque las señales que
obtendría, es decir, esas ondas gravitacionales, se generaría en
regiones donde la gravedad es muy fuerte. Nos permitiría probar el régimen de campo fuerte de la relatividad general, que es algo que no hemos podido hacer hasta ahora. Esto pondría pruebas muy sólidas sobre la relatividad general, por lo que es muy importante que [observemos] los agujeros negros: [las observaciones nos darían] una ventana completamente nueva a la relatividad general.




