Importancia
Científicos y gerentes por igual se han preocupado por la cuestión de si los grupos de solucionadores de problemas que interactúan superan a los individuos autónomos y, de ser así, en qué condiciones. Aquí describimos un experimento en el que se evaluó a individuos y grupos en una serie de tareas de diversa complejidad. Encontramos que los grupos son tan rápidos como el individuo más rápido y más eficientes que el individuo más eficiente cuando la tarea es compleja pero no cuando la tarea es simple. Luego, cuantificamos con precisión las ganancias sinérgicas y las pérdidas de procesos asociadas con los grupos que interactúan, y descubrimos que el equilibrio entre los dos depende de la complejidad. Nuestro estudio tiene el potencial de conciliar hallazgos contradictorios sobre la sinergia grupal en trabajos anteriores.
Resumen
La complejidad, definida en términos del número de componentes y la naturaleza de las interdependencias entre ellos, es claramente una característica relevante de todas las tareas que realizan los grupos. Sin embargo, el papel que juega la complejidad de la tarea en la determinación del desempeño del grupo sigue siendo poco conocido, en parte porque no existe un lenguaje claro para expresar la complejidad de una manera que permita comparaciones directas entre tareas. Aquí evitamos esta dificultad analítica al identificar una clase de tareas para las cuales la complejidad se puede variar sistemáticamente mientras se mantienen todos los demás elementos de la tarea sin cambios. Luego probamos los efectos de la complejidad de la tarea en un experimento de dos fases registrado previamente en el que se evaluó a 1200 personas en una serie de tareas de complejidad variable (fase 1) y luego se les asignó aleatoriamente para resolver tareas similares en grupos interactivos o como individuos independientes ( fase 2). Encontramos que los grupos que interactúan son tan rápidos como el individuo más rápido y más eficientes que el individuo más eficiente para tareas complejas pero no para las más simples. Aprovechando nuestros datos digitales altamente granulares, definimos y medimos con precisión las pérdidas de procesos grupales y las ganancias sinérgicas y mostramos que el equilibrio entre los dos interruptores muestra valores intermedios de complejidad de tareas. Finalmente, encontramos que los grupos que interactúan generan más soluciones más rápidamente y exploran el espacio de solución más ampliamente que los solucionadores de problemas independientes, encontrando soluciones de mayor calidad que todos excepto los individuos con puntajes más altos.
Las tareas realizadas por grupos de solucionadores de problemas que interactúan, ya sea en el mundo real o en entornos experimentales, varían según una serie de dimensiones que posiblemente influyen en el desempeño del grupo (1⇓⇓⇓⇓–6). En este artículo, nos centramos en una dimensión importante pero empíricamente poco estudiada de las tareas, la complejidad, que generalmente se entiende que depende de al menos dos factores: (i) el número de componentes distintos que constituyen una tarea y (ii) el número, la fuerza , y configuración de interdependencias entre esos componentes (7⇓⇓⇓–11).
Intuitivamente, la complejidad de la tarea tiene una relevancia obvia para el desempeño del grupo. En igualdad de condiciones, uno esperaría que los solucionadores de problemas se desempeñen peor en tareas que tienen más componentes o para las cuales las interacciones entre los componentes son más densas. Además, también se podría esperar que la complejidad de la tarea impacte en la "sinergia" del grupo, definida como un rendimiento superior al que se esperaría para una colección de individuos de tamaño similar que trabajan de forma independiente, también conocido como "grupo nominal" (12). En este caso, sin embargo, es menos obvio cuál sería la dirección del efecto. Por un lado, los grupos que interactúan pueden desempeñarse mejor en relación con los grupos nominales en tareas complejas porque pueden distribuir el esfuerzo (13), compartir información sobre soluciones de alta calidad (14) o corregir errores (15). Por otro lado, con tareas más complejas, los grupos que interactúan pueden experimentar pérdidas de proceso aún mayores, incluidos holgazanería social (16), pensamiento grupal (17) y conflicto interpersonal (4), posiblemente porque las tareas complejas exigen más de los contribuyentes individuales y ofrecen más oportunidades de quedar atrapado en niveles óptimos locales globalmente subóptimos, cualquiera de los cuales también podría conducir a un mayor estrés y bajo rendimiento en relación con los grupos nominales.
Un desafío importante para resolver preguntas sobre los efectos de la complejidad de las tareas es que, si bien el concepto de alto nivel parece intuitivo, aún no se ha puesto en práctica con la precisión suficiente para permitir a los investigadores cuantificar la complejidad de los diferentes tipos de tareas y, por lo tanto, hacer manzanas. a las manzanas comparaciones entre ellos. Más bien, las operacionalizaciones existentes son a menudo complejas. Por ejemplo, un modelo enumera 27 factores que contribuyen a la complejidad agrupados en 10 dimensiones de complejidad (9), mientras que otros modelos son lo suficientemente específicos del dominio como para que las diferencias numéricas entre diferentes tipos de tareas sean difíciles de interpretar (7). Agregando confusión, algunas definiciones enfatizan la complejidad objetiva, refiriéndose solo a las características de la tarea que se pueden medir independientemente de quienes la realizan, mientras que otras enfatizan la complejidad subjetiva, la complejidad de la tarea tal como la experimentan quienes la realizan (9, 11).
Aquí evitamos estas dificultades analíticas al identificar una clase de tareas para las cuales la complejidad se puede variar sistemáticamente mientras se mantienen fijos todos los demás elementos de la tarea. De esta forma, podemos medir fácilmente el rendimiento en función de la complejidad creciente sin preocuparnos por los factores de confusión que surgen de otros aspectos de la tarea, como el tipo de tarea (3) u otras características de los procesos grupales (4, 18). Además, requerimos que nuestras tareas se puedan realizar de manera realista, ya sea de forma independiente o en colaboración, lo que permite una comparación directa entre grupos nominales e interactivos.
Una clase de tareas que satisfacen estos criterios son los problemas de optimización y satisfacción de restricciones (CSOP), que se estudian ampliamente en inteligencia artificial e investigación de operaciones. La conexión con la investigación de operaciones es útil porque, a diferencia de otros problemas de "juguete", los CSOP se asignan de una manera relativamente intuitiva a una gama de problemas prácticos de asignación de recursos y se han utilizado para modelar muchos problemas que son de interés práctico. Los ejemplos de CSOP incluyen proyectos de software de dotación de personal donde hay varias asignaciones potenciales de desarrollador a actividad para evaluar (19); formar grupos de aprendizaje en base a algunos criterios relacionados con los objetivos de la colaboración (20); horarios de trenes (21); y la asignación de vacunas, ventiladores y suministros médicos durante la pandemia de COVID-19 (22). Además, si bien los CSOP capturan características importantes de los ejercicios de resolución de problemas grupales del mundo real, no requieren que los participantes tengan habilidades especializadas. Como resultado, los participantes pueden ser reclutados a partir de servicios en línea, lo que reduce el costo y la dificultad de coordinar la participación simultánea de grupos. Finalmente, al igual que con otros problemas complejos (14, 23⇓–25), la función de pago de los CSOP se puede describir como un panorama de rendimiento accidentado, donde cada punto del panorama representa una combinación de opciones potencialmente interdependientes (una solución al problema) , mientras que la altura del punto representa el desempeño de esa combinación (26, 27). Por lo tanto, los CSOP pueden caracterizarse por varias soluciones localmente óptimas pero globalmente subóptimas (26, 27) y, por lo tanto, son susceptibles de muchas estrategias y estilos de solución potenciales, sin una única estrategia universalmente superior (28).
El CSOP específico que estudiamos es un problema de asignación de habitaciones en el que los participantes, ya sea individualmente o en grupos, asignan N estudiantes a M habitaciones donde cada estudiante tiene una utilidad específica para cada habitación (Apéndice SI, sección 1.1). El objetivo de la tarea es maximizar la utilidad total del estudiante respetando al mismo tiempo las restricciones Q (por ejemplo, "Los estudiantes A y J no pueden compartir una habitación o estar en habitaciones adyacentes"). Cuando la tarea se realiza en grupos, los participantes pueden comunicarse a través de un chat basado en texto y mover a diferentes estudiantes simultáneamente, realizando así un procesamiento paralelo si así lo desean. De manera crítica para nuestros propósitos, la complejidad de la tarea se puede variar sistemáticamente ajustando solo tres parámetros clave: el número de estudiantes , el número de habitaciones y el número de restricciones . De hecho, una ventaja significativa de esta tarea (y de los CSOP en general) sobre las tareas que se estudian más comúnmente en entornos de desempeño grupal es que su complejidad se puede cuantificar en términos del tiempo de ejecución requerido por un solucionador algorítmico para encontrar la solución óptima, lo que permite nosotros para clasificar fácilmente instancias de tareas por complejidad (consulte Materiales y métodos para obtener más detalles). La figura 1 ilustra cómo se puede variar la complejidad entre dos instancias del problema de asignación de habitaciones. En una instancia de baja complejidad, se deben asignar seis estudiantes a cuatro habitaciones sujetas a solo dos restricciones ("B y E deben ser vecinos" y "C y F no pueden vivir en la misma habitación"). En una instancia de alta complejidad, se deben asignar 18 estudiantes a 8 salas sujetas a 18 restricciones.
Ilustración de la tarea de asignación de habitaciones. La tarea requería asignar N estudiantes a M salas para maximizar la utilidad total de los estudiantes, cada uno de los cuales tiene una utilidad específica para cada sala, respetando al mismo tiempo las restricciones Q. La complejidad de la tarea se caracteriza por la cantidad de estudiantes a los que se les asignará , la cantidad de dormitorios disponibles y la cantidad de restricciones
Diseño de experimentos
En este artículo, probamos la hipótesis de que la complejidad de la tarea modera el rendimiento relativo de la resolución de problemas en grupo frente a la individual. Con este fin, abordamos la siguiente pregunta: ¿cómo el equilibrio entre las pérdidas del proceso y las ganancias sinérgicas en los grupos que interactúan depende de la complejidad de la tarea?
Nuestro experimento se desarrolló en dos fases. En la fase 1, 1200 participantes completaron individualmente cinco tareas de asignación de habitaciones: tres tareas de complejidad muy baja y dos de complejidad moderada (Apéndice SI, Tabla S1), así como una prueba estándar de Lectura de la mente en los ojos (Apéndice SI, sección S1.2 y Fig. S3), que se usa comúnmente como una medida de la percepción social y fue utilizado por varios estudios recientes que relacionan la percepción social con el desempeño del grupo (18, 29⇓⇓–32).
Después de completar la fase 1, calificamos a todos los participantes en el nivel de habilidad y percepción social para poder asignarlos a bloques experimentales en la fase 2 (Apéndice SI, sección 1.4 y Fig. S4). Al tener en cuenta estas características en nuestro procedimiento de aleatorización por bloques en la fase 2, pudimos asegurarnos de que varios niveles de habilidad y percepción social (y combinaciones de los mismos) estuvieran equilibrados en los arreglos de trabajo grupales e individuales. El objetivo principal del esquema de aleatorización en bloques era sobremuestrear combinaciones estadísticamente menos frecuentes (p. ej., todos los miembros del grupo con altas habilidades o alta percepción social), aumentando así el poder estadístico de nuestros experimentos. Notamos que nuestro enfoque aquí está en la comparación entre los grupos que interactúan y los nominales, no en las diferencias de composición entre los grupos que interactúan; por lo tanto, nuestro análisis de los efectos del nivel de habilidad y la percepción social sobre el desempeño se publicará en otro lugar (según nuestro registro previo).
Se invitó a los mismos 1200 participantes a participar en la fase 2, y los primeros 828 participantes que se presentaron y pasaron los controles de atención (según nuestra preinscripción; consulte el Apéndice SI, Tabla S2, para tamaños de muestra) fueron asignados a un segundo secuencia de cinco tareas de asignación de habitaciones (la secuencia de tareas fue aleatoria), también de complejidad variable (muy baja, baja, moderada, alta y muy alta; Apéndice SI, Tabla S3 y Fig. S5). Todas las tareas expiraron a los 10 min en la fase 2, independientemente de su complejidad. Con base en la habilidad y la percepción social de cada participante según lo medido en la fase 1, primero asignamos a cada individuo en bloques (por ejemplo, alta habilidad, alta percepción social; habilidad mixta, alta percepción social, etc.). A continuación, dentro de cada bloque, los participantes se asignaron al azar a una de dos condiciones: una condición de grupo interactivo ( participantes, formando 197 grupos de tamaño 3; los datos de 1 grupo están incompletos, lo que lleva al número de grupos interactivos válidos siendo 196), en el que los miembros del grupo resolvieron el problema colectivamente y pudieron comunicarse entre sí a través de un chat basado en texto; y una condición individual independiente ( participantes; los datos de 3 individuos están incompletos, lo que lleva a que el número de individuos independientes válidos sea 234), en la que cada participante trabajó solo en su tarea asignada. Todos los resultados presentados aquí son de la fase 2 del experimento.
Evaluación de desempeño.
En la fase 2, usamos tres métricas para capturar el rendimiento en una instancia de tarea de asignación de sala: (1) puntaje normalizado, definido como el puntaje real obtenido en una instancia de tarea dividido por el puntaje máximo posible para esa tarea; (2) duración (o tiempo hasta la finalización), definida como el tiempo transcurrido desde el inicio de la tarea hasta que se presentó una solución (o hasta que la tarea se agota a los 10 min); y finalmente, (3) eficiencia, definida como la puntuación normalizada dividida por la duración.
Las tres métricas son indicadores naturales de rendimiento que uno puede desear optimizar en algunas circunstancias. En ausencia de limitaciones de tiempo, por ejemplo, la puntuación normalizada es una medida obvia de la calidad de la solución. Por el contrario, la duración es apropiada cuando el tiempo de resolución de problemas es más importante que la calidad (por ejemplo, elaborar rápidamente un plan razonablemente bueno para la asignación de recursos en una respuesta a un desastre), y la eficiencia es apropiada cuando tanto la calidad como la velocidad son importantes (por ejemplo, , en el desarrollo de productos).
Después de un trabajo previo (12, 33⇓⇓⇓–37), evaluamos el desempeño del grupo en comparación con los llamados grupos nominales, definidos como una colección de individuos autónomos de tamaño similar. Los grupos nominales proporcionan un punto de referencia útil para los grupos que interactúan porque dan cuenta de la disponibilidad diferencial de recursos entre grupos e individuos (12); es decir, se ajustan por la cantidad de recursos intelectuales que los grupos podrían aportar (es decir, horas de trabajo) y la probabilidad matemática de que al menos un miembro podría haber logrado el mismo desempeño. Por lo tanto, el desempeño del grupo que interactúa por encima del de un grupo nominal puede atribuirse a la interacción del grupo, no a mayores recursos.
En general, las comparaciones entre grupos que interactúan y grupos nominales de tamaño equivalente han encontrado evidencia contradictoria de efectos sinérgicos (12): mientras que los grupos que interactúan a menudo superan al miembro promedio de un grupo nominal (sinergia débil), rara vez superan al mejor miembro ( fuerte sinergia). Reflejando esta distinción, comparamos nuestros grupos interactivos con cuatro puntos de referencia de desempeño, cada uno de los cuales corresponde a un grupo nominal distinto construido al seleccionar tres individuos al azar y sin reemplazo del mismo bloque. El primer punto de referencia corresponde al puntaje de desempeño de un miembro elegido al azar del grupo nominal (equivalente a un individuo promedio), mientras que los tres restantes corresponden al individuo con el mejor desempeño de la fase 1 en cada una de las tres métricas definidas anteriormente (es decir, la puntuación más alta, la duración más baja y la eficiencia más alta). Por lo tanto, los grupos nominales simulan una situación en la que un gerente asigna el trabajo a un individuo al azar, al individuo con la puntuación más alta, al individuo más rápido o al individuo más eficiente, a juzgar por el desempeño anterior (es decir, puntajes de la fase 1, duraciones y eficiencias).
Resultados
Rendimiento en función de la complejidad de la tarea.
Fig. 2 muestra cómo varió el rendimiento en función de la complejidad de la tarea. En todas las condiciones, la mayor complejidad de la tarea resultó en puntajes normalizados más bajos (Fig. 2A), mayor duración (Fig. 2B) y, por lo tanto, menor eficiencia (Fig. 2C). Estas tendencias de rendimiento también se mantienen cuando se miden por separado para grupos interactivos y nominales (Apéndice SI, sección S2 y Fig. S7). En promedio, los individuos y los grupos dedicaron aproximadamente tres veces más tiempo a la tarea más compleja que a la tarea menos compleja, pero obtuvieron puntajes normalizados que fueron aproximadamente 10 puntos porcentuales más bajos. Dado que las puntuaciones normalizadas casi siempre superaban los 80, esta última diferencia representa aproximadamente el 50% del rango efectivo, un efecto grande. La clara dependencia monótona de las tres medidas de desempeño en la complejidad es importante por dos razones. Primero, valida nuestro diseño, demostrando que los aumentos en la complejidad capturados por los cambios en los parámetros de la tarea N, M y Q se traducen de manera directa en la complejidad que experimentan nuestros participantes. En segundo lugar, ofrece una ventaja considerable para probar nuestra predicción de que el rendimiento relativo de los grupos que interactúan frente a los grupos nominales depende de la complejidad de la tarea.
Variar la complejidad de la tarea de asignación de salas. El aumento de la complejidad de la tarea (A) reduce la puntuación normalizada, (B) aumenta el tiempo necesario para completar la tarea y (C) reduce la eficiencia. Los datos se combinan en condiciones individuales y grupales en los seis bloques. Las barras de error indican los intervalos de confianza del 95% (algunos no son lo suficientemente grandes como para mostrarlos). Los grupos e individuos obtuvieron al menos el 80 % de la puntuación máxima en más del 85 % de las tareas; por lo tanto, el rango efectivo para la puntuación normalizada (es decir, el eje y de A) está entre 80 y 100 %. El tiempo mínimo requerido para que se presente una solución es de 1 min y el máximo de 10 min; por lo tanto, el rango efectivo para la duración (es decir, el eje y de B) está entre 1 y 10 min. La diferencia en la dificultad experimentada entre la complejidad muy baja y la muy alta es muy grande: la puntuación media normalizada se redujo en aproximadamente un 50 % del rango efectivo de puntuaciones (de aproximadamente el 95 al 85 % en una escala efectiva de 80 a 100), y la el tiempo medio empleado aumentó en un 200 % (de 2 a 6 min).
Evidencia de sinergia de grupo.
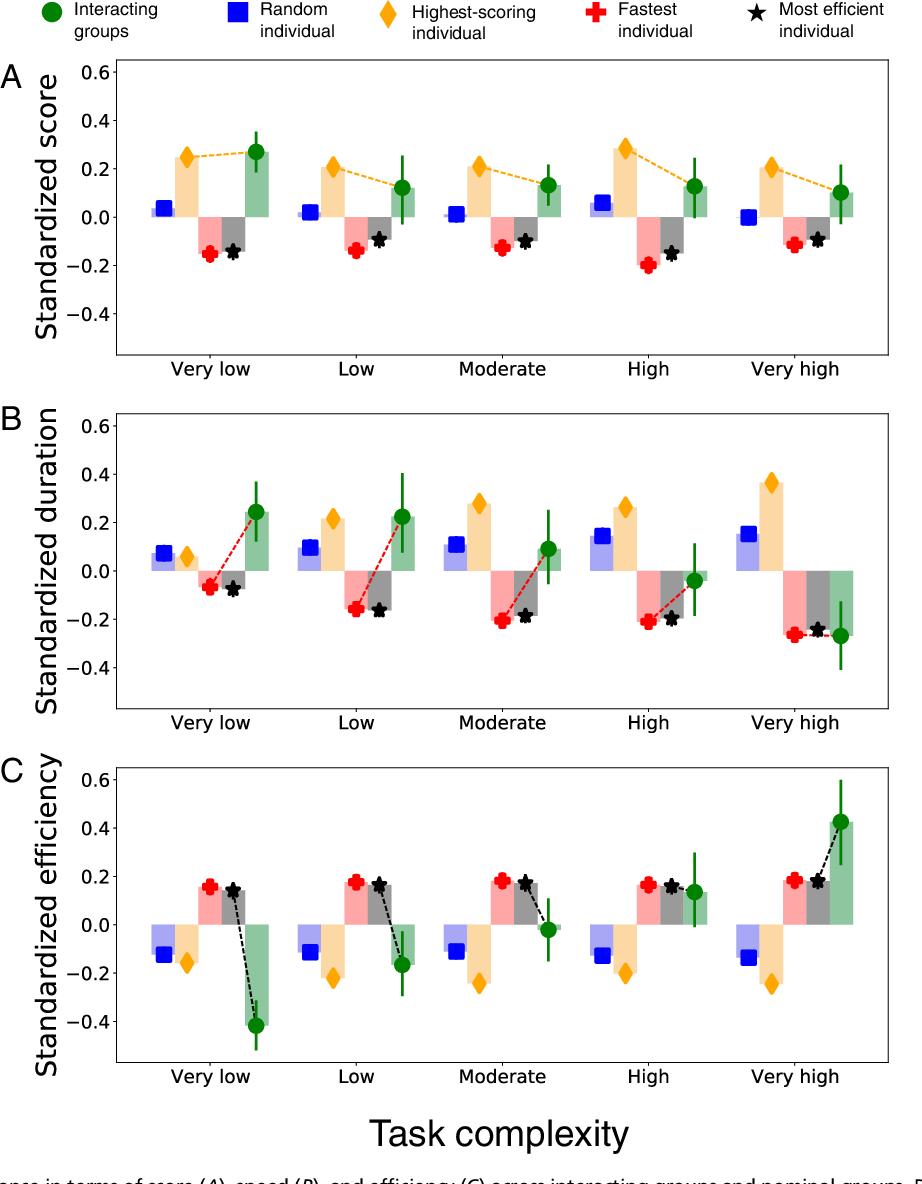
Fig. 3 compara el desempeño general del grupo estandarizado (transformado a puntajes z dentro de cada nivel de complejidad de la tarea) con las cuatro definiciones de grupo nominal: individuo aleatorio, individuo con puntaje más alto, individuo más rápido e individuo más eficiente.
Comparar el rendimiento en términos de puntaje (A), velocidad (B) y eficiencia (C) entre grupos interactivos y grupos nominales. Los datos se combinan en los seis bloques y se estandarizan (es decir, se transforman en puntajes z) dentro de cada nivel de complejidad de la tarea (las diferencias son relativas dentro del nivel de complejidad y no deben compararse entre niveles de complejidad). Las barras de error indican los intervalos de confianza del 95%. Hemos repetido los análisis presentados en esta figura para cada bloque, con resultados cualitativamente similares (Apéndice SI, sección S3 y Figs. S8–S10).
Rendimiento como calidad de la solución.
Para todos los niveles de complejidad de la tarea, la Fig. 3A muestra que los grupos obtienen una puntuación más alta que los miembros seleccionados al azar, más rápidos y más eficientes de grupos nominales de tamaño equivalente ( P = 0,013, IC del 95 % [0,026, 0,225]; P < 0,001, IC del 95 % [0,184, 0,410]; P < 0,001, IC del 95 % [0,155, 0,378]; respectivamente) pero menor que la puntuación más alta miembro (P = 0,047, IC del 95 % [−0,159, −0,001]; véanse las tablas de regresión en el apéndice SI, tablas S4–S7). Este resultado es consistente con hallazgos de larga data (33⇓⇓⇓–37) de que los grupos que interactúan a menudo superan a los grupos nominales en términos de calidad de la solución cuando el estándar lo establece un criterio de miembro promedio (sinergia débil), pero no cuando lo establece un criterio de mejor miembro (sinergia fuerte).
Rendimiento como velocidad.
Fig. 3B muestra que los grupos que interactúan completan tareas más complejas, pero no las más simples, más rápido que los miembros aleatorios y los que obtienen la puntuación más alta de grupos nominales de tamaño equivalente. Además, los grupos que interactúan son tan rápidos como los miembros más rápidos y eficientes en la tarea de mayor complejidad (consulte el Apéndice SI, Tablas S8–S10, para tablas de regresión). Estos sugieren que, de hecho, para tareas con muchos componentes (estudiantes y aulas) e interdependencias densas (muchas restricciones), los beneficios de distribuir el trabajo a un grupo podrían superar las pérdidas del proceso asociadas con la interacción de grupos, lo cual es consistente con los hallazgos en trabajos anteriores ( 36).
Rendimiento como eficiencia.
Finalmente, la Fig. 3C muestra que para las tareas más complejas las ganancias en velocidad superan los déficits en la puntuación. Esto da como resultado una sorprendente interacción entre la complejidad de la tarea y la organización del trabajo: mientras que los grupos que interactúan son considerablemente menos eficientes que los miembros seleccionados de los grupos nominales en tareas simples, su eficiencia relativa aumenta con la complejidad de la tarea hasta que superan a los de mayor puntuación, más rápidos y más eficientes. miembros en la complejidad más alta (ver Apéndice SI, Tablas S11–S13, para tablas de regresión). Este resultado recuerda a la toma de decisiones en grupo entre insectos sociales en el que un estudio reciente ha encontrado que las colonias de hormigas superan a las hormigas individuales cuando la tarea de discriminación es difícil pero no cuando es fácil (38).
Desempaquetando la sinergia grupal.
El hallazgo de que los grupos que interactúan son más eficientes que los miembros mejor seleccionados de grupos nominales de tamaño equivalente, según cualquiera de nuestras cuatro definiciones, cuando la tarea es compleja, pero no cuando la tarea es simple, sugiere que el equilibrio entre las pérdidas del proceso y las ganancias sinérgicas depende de la complejidad de la tarea. Para entender mejor esta dependencia, y observando que la variación en la eficiencia aparente en la (Fig. 2C) depende más de la variación en la duración de la tarea (que varía entre 2 y 6 min en promedio, Fig. 2B) que de la variación en la puntuación obtenida (que varía entre 95% y 85% en promedio, Fig. 2A), a continuación presentamos un análisis exploratorio del tiempo empleado en cada etapa de resolución de la tarea. Este análisis es posible gracias a la naturaleza altamente granular de nuestros datos. Debido a que cada acción realizada por cada participante tiene una marca de tiempo, podemos dividir el tiempo de solución general en segmentos medidos con mucha precisión que corresponden a distintas etapas del proceso de resolución de problemas. Para mayor claridad, definimos cuatro segmentos clave, ilustrados esquemáticamente en la Fig. 4A:
Hitos de finalización de tareas. (A) Los cuatro hitos en el proceso de resolución de problemas: (i) se genera la primera solución intermedia, (ii) se genera la mejor solución intermedia, (iii) se genera la solución final, y (iv) se genera la solución final enviado. (B, D, F y H) El tiempo empleado (en minutos) por grupos e individuos (ya sea al azar, con la puntuación más alta, más rápida o más eficiente) en cada segmento de tiempo. (C, E, G e I) El tiempo estandarizado empleado (transformado en puntajes z; es decir, mostrando la diferencia relativa dentro del nivel de complejidad) en cada segmento de tiempo. Las barras de error indican los intervalos de confianza del 95%.
Tiempo hasta la primera solución, .
El tiempo desde el comienzo de la tarea hasta la generación de la primera solución puede verse como el tiempo dedicado a formular una estrategia para abordar la tarea.
Tiempo para la mejor solución, .
La mejor solución no es necesariamente la que se envió porque la instancia de la tarea solo finaliza una vez que un grupo/individuo decide enviarla una solución, y los grupos/individuos pueden generar soluciones después de su mejor solución sin volver a ella.
Tiempo desde la solución óptima hasta la solución final, .
El tiempo transcurrido entre la generación de la solución óptima y la solución final, que puede verse como "exceso de exploración". disminuye la eficiencia ya que conduce a una calidad de solución inferior (o igual) pero a una mayor duración total de la tarea.
Tiempo desde la solución final hasta el envío, .
El tiempo transcurrido entre la generación de la solución final y la decisión de enviarla, que puede verse como " tiempo de compromiso”, puede ser otra fuente de ineficiencia, ya que conduce a una calidad de solución igual pero aumenta la duración total de la tarea.
fig. 4 muestra dos conjuntos de comparaciones entre grupos interactivos y nominales para cada uno de estos cuatro segmentos. La figura 4 B, D, F y H muestran las duraciones sin procesar para , , y
Primero, observamos que (en promedio) los grupos que interactúan pasan menos tiempo en (tiempo hasta la primera solución, Fig. 4 B y C) que los miembros de los grupos nominales independientemente de la complejidad de la tarea ( para todos; y Apéndice SI, Tabla S14). Especulamos que esta observación puede estar relacionada con los argumentos de estudios recientes de que la pertenencia a un grupo reduce el sentido de responsabilidad y el arrepentimiento que los miembros pueden enfrentar en las mismas circunstancias individualmente. Si es correcto, una barrera emocional reducida para la acción puede ser un mecanismo subyacente que impulsa a los miembros del grupo a actuar antes (39).
En segundo lugar, observamos un efecto notable de la complejidad de la tarea en (tiempo para la mejor solución, Fig. 4 D y E): los grupos que interactúan tardan más en llegar a la mejor solución que los más rápidos. y los miembros más eficientes de los grupos nominales para la tarea menos compleja pero más rápidos para la tarea más compleja (P < 0,001, IC del 95 % [0,119, 0,385] y [0,109, 0,371], respectivamente, en la complejidad más baja, y P < ; 0,001, IC del 95 % [−0,351, −0,085] y [−0,370, −0,108], respectivamente, en la mayor complejidad; consulte las Tablas S17–S18 del Apéndice SI para las tablas de regresión). Es importante destacar que observamos que la mayor parte de la duración de la tarea se dedica a este segmento, lo que sugiere que la velocidad para encontrar la mejor solución es el principal contribuyente a la sinergia del grupo. Una posible explicación de por qué los grupos que interactúan son más rápidos para encontrar la mejor solución a alta complejidad es que los grupos que interactúan obtienen algunos beneficios de la división del trabajo (consulte el Apéndice SI, sección S4 y la Fig. S11, para obtener evidencia sugerente). Otra posible explicación, para la cual vemos alguna evidencia anecdótica en los registros de chat (Apéndice SI, Fig. S11), es que los grupos que interactúan están más dispuestos a satisfacer aceptando una solución actualmente disponible como satisfactoria (40). Otra podría ser que se beneficien de la toma de turnos, en la que una persona es principalmente activa, mientras que los demás están considerando su(s) próximo(s) movimiento(s). Desafortunadamente, el diseño experimental actual no nos permite discriminar entre estas explicaciones alternativas, por lo que siguen siendo especulativas.
Tercero, observamos que, independientemente de la complejidad, los grupos que interactúan pasan más tiempo en el segmento (exceso de exploración, Fig. 4 F y G) en relación con los miembros de los grupos nominales; al igual que con , la diferencia es constante en todos los niveles de complejidad (consulte el Apéndice SI y las Tablas S19–S20 para las tablas de regresión). En cuarto lugar, los grupos que interactúan también dedican más tiempo a comprometerse con una solución () que los miembros seleccionados de los grupos nominales, una vez más, independientemente de la complejidad (Fig. 4 H e I y SI Apéndice, Tabla S14) . Especulamos que el hecho de que los grupos que interactúan puedan comunicarse a través del chat (y carecer de un líder asignado) puede agregar presión a los grupos para garantizar que sus decisiones se tomen colectivamente (es decir, llegar a un consenso), lo que podría contribuir al efecto observado.
En quinto lugar, observamos que la duración media total de la tarea oscila entre min con una complejidad muy baja y min con una complejidad muy alta (de un máximo de 10 min), lo que significa que los participantes generalmente envían la solución y finalizan la instancia de la tarea antes de quedarse sin tiempo. Esta observación es relevante para nuestro análisis en el sentido de que nuestras comparaciones de rendimiento de los grupos que interactúan con el de los miembros seleccionados de los grupos nominales no se ven afectadas por la restricción de tiempo.
En resumen, la Fig. 4 revela dos tipos de pérdidas de procesos (es decir, el tiempo adicional dedicado a la exploración excesiva y el logro de consenso) y dos tipos de sinergias (es decir, tiempo más rápido para la primera solución y tiempo más rápido para la mejor solución para tareas complejas ). Curiosamente, mientras que las sinergias, específicamente en el tiempo para la mejor solución, dependen de la complejidad de la tarea, las pérdidas del proceso no. En otras palabras, nuestros hallazgos sugieren que estar en un grupo interactivo tiene costos fijos que son relativamente consistentes a través de los niveles de complejidad de la tarea, pero un beneficio que varía según los niveles de complejidad (es decir, menos tiempo dedicado a encontrar la mejor solución).
Para aclarar aún más este hallazgo, a continuación agregamos los costos y beneficios para cuantificar el valor de realizar la tarea en un grupo que interactúa en todos los niveles de complejidad. En particular, medimos cada costo y beneficio como la diferencia absoluta, en términos de tiempo invertido, entre los grupos que interactúan y el miembro aleatorio (es decir, el promedio) de los grupos nominales en cada segmento de tiempo:
fig. 5 muestra que el costo total asociado con las ineficiencias de los grupos que interactúan (es decir, exploración excesiva, llegar a un consenso) excede los beneficios sinérgicos (es decir, ganancias de velocidad para encontrar la mejor solución) cuando se resuelven tareas de baja complejidad pero no de alta complejidad. Esto explica nuestro hallazgo de que los grupos son más eficientes que los miembros más rápidos, eficientes y con puntaje más alto de grupos nominales de tamaño equivalente cuando la tarea es compleja, pero que esta relación se invierte cuando la tarea es simple. Encontramos resultados similares para la comparación de miembros con la puntuación más alta (Apéndice SI, sección S5 y Fig. S12).
El costo-beneficio de los grupos interactivos. La figura ilustra la diferencia absoluta en términos de tiempo promedio empleado entre los grupos que interactúan y un grupo nominal individual promedio en cada segmento de tiempo.
Explorando las diferencias en los enfoques de resolución de problemas.
Recapitulando nuestros resultados principales, los grupos que interactúan son más eficientes que incluso el miembro más eficiente de los grupos nominales para problemas de alta complejidad; por lo tanto, concluimos que muestran una fuerte sinergia para la eficiencia (Fig. 3C). Con respecto a la velocidad, los grupos que interactúan son más rápidos que el miembro promedio (elegido al azar) y tan rápidos como el miembro más rápido de los grupos nominales de tamaño equivalente (Fig. 3B), mostrando así solo una sinergia débil. Para la calidad de la solución, los grupos que interactúan muestran una sinergia aún más débil, ya que obtienen una puntuación más alta que el miembro promedio, pero no tanto como el miembro con la puntuación más alta de los grupos nominales (Fig. 3A).
Para investigar más a fondo estos resultados, examinamos la cantidad y el ritmo de las soluciones intermedias generadas, donde una solución intermedia se define como una asignación de estudiantes a las salas (es decir, cada acción realizada por un participante genera una solución intermedia). Como se muestra en la Fig. 6 A y B, observamos que los grupos no solo generaron más soluciones intermedias que los miembros aleatorios, de mayor puntuación, más rápidos y más eficientes de grupos nominales de tamaño equivalente ( para todos, los IC del 95 % , , y respectivamente, Apéndice SI, Tabla S23); también lo hicieron a una tasa más alta ( para todos, IC del 95 % , , y , respectivamente; Anexo SI, Tabla S23). Los grupos que interactúan también exhibieron un radio de solución más amplio, definido como la distancia de edición máxima (es decir, la cantidad de diferencias en las asignaciones de estudiantes/salas) entre la primera solución completa (es decir, todos los estudiantes asignados a las salas pero los conflictos pueden quedar sin resolver) y todas las subsiguientes. soluciones completas, lo que sugiere que exploraron el espacio de soluciones de manera más amplia (Fig. 6C; para todos, IC del 95 % , , y respectivamente; Anexo SI, Tabla S23). También confirmamos esta conclusión cualitativa usando otras dos medidas de exploración: el porcentaje de soluciones dentro de una distancia de edición de dos de la solución final y el porcentaje de soluciones intermedias que involucraron una violación de restricción (Apéndice SI, Figs. S13 y S14).
Diferencias mecánicas en los enfoques de resolución de problemas entre grupos e individuos que interactúan. Los grupos que interactúan generan (A) más soluciones, (B) a un ritmo más rápido y (C) exploran el espacio de soluciones de manera más amplia. (D) Sin embargo, la calidad de la mejor solución encontrada (ya sea presentada o no) no es mejor que la solución encontrada por los grupos nominales de individuos con la puntuación más alta. Las barras de error indican los intervalos de confianza del 95%.
A la luz de estas observaciones, es aún más sorprendente que los grupos que interactúan no encontraron soluciones de mayor calidad que el miembro con la puntuación más alta de los grupos nominales (Fig. 6D; ; Apéndice SI, Tabla S23). En parte, la brecha se puede explicar porque los grupos que interactúan tampoco envían su mejor solución encontrada a un ritmo más alto que el individuo con la puntuación más alta: en todas las complejidades, el individuo con la puntuación más alta no envía su solución mejor encontrada
¿Qué podría explicar la combinación de una fuerte sinergia en la eficiencia y una sinergia débil en la calidad y la velocidad de la solución? La investigación previa que conceptualiza la resolución de problemas como una búsqueda adaptativa en un paisaje de rendimiento accidentado (14, 27), en el que cada punto del paisaje representa una solución para la asignación de la habitación y la altura del punto representa el desempeño de esa tarea, proporciona varios, posiblemente interrelacionadas, explicaciones. Una posible explicación es que los individuos con puntajes más altos tienen mejores representaciones (aproximaciones de menor dimensión) del verdadero panorama de desempeño, lo que les permite evaluar soluciones (y trayectorias de soluciones) fuera de línea sin probarlas a través de la experimentación (41, 42). Mejores representaciones pueden conducir a evaluaciones fuera de línea más precisas y esfuerzos de búsqueda más efectivos (26, 43, 44), caracterizados por menos soluciones intermedias y mayor calidad de solución. Alternativamente, los grupos de solucionadores de problemas pueden tener intereses en conflicto (p. ej., maximizar la puntuación versus minimizar la duración) y, por lo tanto, diferentes visiones del curso de acción correcto (45). Si es cierto, los grupos podrían beneficiarse de la coordinación central mediante la asignación de un líder de grupo (45) o de intervenciones relacionadas con el proceso, como imponer pausas intermitentes en la interacción (46, 47). Otra posibilidad más es que cuando el tiempo es limitado, las estrategias de búsqueda que permiten ganancias rápidas (es decir, grandes mejoras en el rendimiento desde el principio) y reducen la cantidad de exploración pueden parecer superiores (26). Por lo tanto, mientras que la estrategia de búsqueda de profundización de la ruta local (por ejemplo, escalar colinas) adoptada por los miembros con puntajes más altos de grupos nominales de tamaño equivalente podría proporcionar beneficios de rendimiento a corto plazo, la estrategia de los grupos interactivos de ampliar el dominio de búsqueda podría ser más ventajosa. a largo plazo (48, 49).
Discusión
Para muchas tareas de interés, los gerentes pueden decidir si asignan una tarea a un grupo interactivo oa un número comparable de personas que trabajan de forma independiente (12). Para entornos como estos, nuestros resultados ofrecen varias perspectivas. En primer lugar, las decisiones sobre cómo asignar el trabajo (a grupos que interactúan oa grupos nominales) deberían depender de la complejidad de la tarea en cuestión y de la forma en que se evalúa el desempeño. Por ejemplo, si un gerente quisiera encontrar una solución viable para un CSOP en el menor tiempo posible, la recomendación sería pedirle a un grupo que resuelva el problema cuando el problema sea complejo, pero pedirle a los solucionadores de problemas independientes cuando sea simple. Cabe señalar que los resultados de duración y eficiencia presentados aquí pueden subestimar cómo funcionaría esto en la práctica. Por ejemplo, si el trabajo se organizara en grupos nominales, ese arreglo aún produciría múltiples soluciones diferentes para que algún gerente decida entre ellas. Aunque nuestra operacionalización de grupos nominales simuló una situación en la que el gerente toma la decisión instantáneamente, hay circunstancias en las que un gerente podría querer considerar los méritos de las diferentes soluciones, y esto llevaría una cantidad de tiempo distinta de cero. Este no es el caso de los grupos interactivos, donde el proceso de decisión ya está incluido en el tiempo transcurrido del ejercicio de resolución de problemas.
En segundo lugar, nuestros hallazgos también sugieren que una posible explicación de por qué las pérdidas de procesos grupales han figurado más prominentemente en los hallazgos de investigación que las ganancias sinérgicas (12) es que los estudios de laboratorio sobre el desempeño grupal generalmente se basan en tareas muy simples. De hecho, la evidencia de laboratorio más clara hasta la fecha de un desempeño grupal superior, aunque rara, proviene de grupos que trabajan en tareas relativamente complejas (13, 46, 50, 51); sin embargo, el hecho de que la complejidad de la tarea no varió sistemáticamente dentro de un solo estudio representa una fuente importante de variación incontrolada en investigaciones anteriores (17, 36).
En tercer lugar, nuestro análisis de cómo los grupos que interactúan y los individuos independientes difieren en el tiempo que dedican a varias partes del proceso de resolución de problemas ofrece una idea de cómo se pueden mejorar los procesos grupales. Por ejemplo, nuestro hallazgo de que los grupos dedican más tiempo a decidir que una tarea se ha completado (es decir, lograr un consenso) sugiere que asignar un líder de grupo con la capacidad de tomar esa decisión unilateralmente, como lo hace un individuo, debería reducir esta fuente de demora. , mejorando así el rendimiento del grupo. Además, nuestro hallazgo de que es menos probable que los grupos que interactúan envíen su mejor solución sugiere que almacenar sus mejores soluciones para que puedan recargarse y modificarse potencialmente en pasos posteriores (una característica omnipresente del software de productividad personal) también debería mejorar su rendimiento ( 46).
Cuarto, nuestro análisis de la dinámica de solución de grupos frente a individuos genera acertijos adicionales para el trabajo futuro. En particular, si los grupos generan más soluciones de manera más rápida y eficiente en un rango más amplio del espacio de soluciones que incluso los individuos con puntajes más altos, ¿por qué no encuentran mejores soluciones?
Finalmente, concluimos que la ciencia del desempeño grupal se beneficiaría de una apreciación más profunda y sistemática de las similitudes y diferencias entre las tareas que se les pide a los grupos que realicen, tanto en el laboratorio como en el campo. Existe la necesidad de una teoría integral y empíricamente fundamentada de las tareas grupales (12). Un programa de investigación que variara sistemáticamente los tipos de tareas junto con los procesos grupales permitidos y otros factores contextuales avanzaría en la ciencia básica de la resolución de problemas grupales al mismo tiempo que abordaría las aplicaciones prácticas.
Materiales y métodos
El estudio fue revisado por el Consejo asesor de ética de investigación de Microsoft y aprobado por el Consejo de revisión institucional de investigación de Microsoft (MSR IRB; Aprobación 0000019). Todos los participantes dieron su consentimiento explícito para participar en este estudio, y el MSR IRB aprobó el procedimiento de consentimiento. Nuestro diseño experimental, el tamaño de la muestra y los análisis que comparan el rendimiento entre los grupos que interactúan y los grupos nominales se registraron previamente antes de la recopilación de los datos (AsPredicted 13123). Todos los demás análisis son exploratorios.
Solucionador algorítmico.
Modelamos cada problema de asignación de habitaciones como un problema de programación de enteros mixtos y generamos el tiempo de ejecución para que las computadoras resuelvan cada problema utilizando el software IBM ILOG CPLEX Optimization Studio, que es un solucionador de programación matemática de alto rendimiento para programación lineal, programación entera mixta y programación cuadrática. El software se ejecutaba en una computadora portátil con un microprocesador Intel Core i5 que funcionaba a una velocidad de 2,6 GHz. Ejecutamos el software usando la configuración predeterminada de parámetros. La unidad del tiempo de ejecución en el archivo de tareas es "ticks", que es la unidad de CPLEX para medir la cantidad de trabajo realizado. La correspondencia de los ticks con la hora del reloj varía según las plataformas (incluido el hardware, el software, la carga de la máquina, etc.), pero dado un problema de programación de enteros mixtos y la configuración de los parámetros, los ticks necesarios para resolver un problema son deterministas. En este sentido, la confiabilidad test-retest del solucionador algorítmico es 1. Consulte el Apéndice SI, sección 1.4.2, para obtener detalles adicionales.
Análisis estadístico.
Debido a que cada grupo (o individuo) que interactuaba completó las cinco tareas de asignación de habitaciones, realizamos pruebas para detectar diferencias entre condiciones a nivel de tarea. Para los efectos de interacción, modelamos los datos utilizando un modelo mixto lineal generalizado para cada resultado (p. ej., puntaje, duración y eficiencia) con un efecto aleatorio para el grupo o identificador individual. Estos modelos dan cuenta de la estructura anidada de los datos. Todas las pruebas estadísticas fueron de dos colas (según nuestro registro previo). Los detalles de las pruebas estadísticas se encuentran en el Apéndice SI, sección S7.
Coeficientes estandarizados.
Para permitir comparaciones significativas de los tamaños de los efectos en tareas de diferentes niveles de complejidad, estandarizamos varias métricas de rendimiento (por ejemplo, puntaje, duración, eficiencia y número de soluciones) dentro de cada nivel de complejidad. Por ejemplo, el valor estandarizado de la medida X, medido para la instancia de tarea i de complejidad c, se define comodonde
Disponibilidad de datos
Los datos y el código de replicación están disponibles en Harvard Dataverse, https://doi.org/10.7910/DVN/RP2OCY (52). El experimento se desarrolló utilizando la plataforma Empirica (53). El código fuente de la tarea de asignación de habitaciones se puede encontrar en https://github.com/amaatouq/room-assignment-csop, y el código fuente de la prueba Reading the Mind in the Eyes se puede encontrar en https://github .com/amaatouq/rme-test.
Agradecimientos
Agradecemos a Valery Yakubovich, Hazhir Rahmandad y James Houghton por sus útiles debates y comentarios. Los autores agradecen a la Fundación Alfred P. Sloan (G-2020-13924) por el apoyo financiero.
Notas al pie
Contribuciones de los autores: A.A., M.Y. y D.J.W. investigación diseñada; A.A., M.Y. y D.J.W. investigación realizada; A.A., M.A., M.Y. y D.J.W. contribuyó con nuevos reactivos/herramientas analíticas; A.A., M.A., M.Y. y D.J.W. datos analizados; y A.A., M.A., M.Y. y D.J.W. escribió el papel.
Los autores declaran no tener intereses en competencia.
Este artículo es una presentación directa de PNAS.
Este artículo contiene información de apoyo en línea en https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2101062118/-/DCSupplemental.
Este artículo de acceso abierto se distribuye bajo Creative Commons Attribution-NonCommercial-NoDerivatives License 4.0 (CC BY-NC-ND).




