We asked cosmologist Pau Figueras everything you've ever wanted to know about black holes. In the other part of the interview he explained what black holes are, physically, and how we hope to observe them. In this second part of the interview, he explains how Einstein's theories predict their existence, and how to describe them mathematically.
Please note that since this interview was conducted, hard evidence for black holes has been detected. It comes from gravitational waves. See Black holes exist! to find out more.
How were black holes first predicted?
Einstein published his [general theory of relativity] in late 1915,
and only a few months later, in early 1916, [Karl]
Schwarzschild found the first solution of the Einstein equations. [By solution we mean some values for the variables describing the curvature of spacetime and the distribution of matter that satisfy the Einstein equations.]
[This solution] describes the gravitational field of a spherically-symmetric body: a black hole.
At that time it wasn't understood that that solution corresponded to a
black hole. In fact even in the 30s the greatest minds of that time,
[including] Einstein himself, despised the idea of a black hole
because it contained a singularity, namely a place where curvature is
so large that even general relativity breaks down. It took nearly 50
years to really understand what a black hole is, and this was done only in the 1960s.
General relativity asserts that massive objects curve spacetime. How do black holes affect the curvature of spacetime?
The strength of the gravitational field is measured in terms of the curvature. And because black holes are very massive and they are very small, their gravity is very strong and [creates] a very large curvature of spacetime.
One way to characterise the curvature is something called the Schwarzschild radius:
where $G_ N$ is Newton's constant [of gravity], $M$ is mass of the object and $c$ is speed of light.
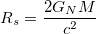
The Schwarzschild radius is, more or less, the size that a given object, with a given mass, should have in order for it to be a black hole. For instance, if we managed to concentrate all the mass of the Earth into a sphere of a radius of a few centimetres, then that object would be a black hole.
Of course we know that this cannot happen because there are other forces in nature which prevent it, but in other circumstances it can happen. For example, when very massive stars run out of nuclear fuel, they cool down and they collapse, and at some point they become small enough so that the whole mass fits within a Schwarzschild radius – therefore they form a black hole.
tyle="font-size:16px;font-family:等线;color:black;background:white">For example, the Schwarzschild radius of the Sun is of the order of a few kilometres. So if we managed to concentrate the whole mass of the Sun into a sphere of a few kilometres, then that would be a black hole.
Can you characterise a black hole so simply, with just a few features, such as mass and size?
One of the reasons why black holes are so important in our understanding of general relativity is because of their simplicity – because they are made of the most fundamental building blocks of the theory, namely space and time alone. They are very simple and therefore we can understand them.
This [is in contrast to] other gravitational objects, such as stars. In order to understand a star, [as well as needing] to take into account general relativity, you also need to understand nuclear physics to account for the nuclear reactions [and] plasma physics to understand the transport of heat within the star. This gets very complicated and we are often led to study these objects within certain approximations.
We don't have to do that with black holes because they are only made of space and time, so we have a complete understanding of them within our theory alone. We don't need any other physics. This simplicity gets translated into the fact that they are just described in terms of very few parameters.
In the vacuum case, if the black hole is static, then it must be spherical and there is only one parameter characterising the black hole, namely its mass. [However], objects in nature, like stars, rotate, so the black holes that occur in nature should have some rotation. The Schwarzschild solution was found [just] months after Einstein published his theory, but it took another 50 years to find the general solution which has rotation and is relevant to describe the black holes [we might find in] nature. This Kerr solution is described entirely by just two parameters, namely the mass and the spin of the black hole. With these two parameters you can fully characterise all black holes in nature and we don't need to make any approximations to understand those objects. This is why they are so important.
In a sense, black holes are no different than elementary particles [in particle physics] because we only need to specify a few parameters [to describe these]. The same with black holes - [they] are the elementary particles of general relativity.
Are black holes the biggest open mystery of general relativity?
Yes. Black holes are a prediction of general relativity and we know of several instances in nature where we think that they should occur, but we haven't detected them yet. So it's still an open question whether they [exist] or not, or whether they have the properties that general relativity predicts.
This is important because most of the tests [of] general relativity [involve] situations where gravity is weak, or relatively weak. For example, we've tested bending of light, the precession of the perihelion of Mercury.
Detecting black holes would be important because the signals that we
would get, namely those gravitational waves, would be generated in
regions where gravity is very strong. It would allow us to test the strong field regime of general relativity, which is something that we haven't been able to do so far. This would put very strong tests on general relativity, so it's very important that we [observe] black holes: [the observations would give us] a completely new window into general relativity.




