Значение
Учените и мениджърите са били заети с въпроса дали и, ако е така, при какви условия групите от взаимодействащи решаващи проблеми превъзхождат автономните индивиди. Тук описваме експеримент, в който индивиди и групи бяха оценени по поредица от задачи с различна сложност. Откриваме, че групите са толкова бързи, колкото и най-бързият индивид и по-ефективни от най-ефективния индивид, когато задачата е сложна, но не и когато задачата е проста. След това прецизно количествено определяме синергичните печалби и загубите на процеса, свързани с взаимодействащи групи, като установяваме, че балансът между двете зависи от сложността. Нашето проучване има потенциала да съгласува противоречиви констатации относно груповата синергия в предишна работа.
Абстракт
Сложността – дефинирана от гледна точка на броя на компонентите и естеството на взаимозависимостите между тях – е очевидно подходяща характеристика на всички задачи, които групите изпълняват. И все пак ролята, която играе сложността на задачата при определяне на ефективността на групата, остава слабо разбрана, отчасти защото не съществува ясен език, който да изрази сложността по начин, който позволява директни сравнения между задачите. Тук избягваме тази аналитична трудност, като идентифицираме клас от задачи, за които сложността може да се променя систематично, като същевременно всички други елементи на задачата остават непроменени. След това тестваме ефектите от сложността на задачата в предварително регистриран двуфазов експеримент, в който 1200 индивида бяха оценени по поредица от задачи с различна сложност (фаза 1) и след това произволно назначени да решават подобни задачи във взаимодействащи групи или като независими индивиди ( фаза 2). Откриваме, че взаимодействащите групи са толкова бързи, колкото и най-бързият индивид и по-ефективни от най-ефективния индивид за сложни задачи, но не и за по-прости. Използвайки нашите силно подробни цифрови данни, ние дефинираме и прецизно измерваме загубите на групови процеси и синергичните печалби и показваме, че балансът между двата превключвателя се намира при междинни стойности на сложността на задачите. И накрая, ние откриваме, че взаимодействащите групи генерират повече решения по-бързо и изследват пространството за решения по-широко от независимите решаващи проблеми, намирайки по-висококачествени решения от всички, освен хората с най-висок резултат.
Задачите, изпълнявани от групи от взаимодействащи решаващи проблеми – независимо дали в реалния свят или в експериментални настройки – варират по редица измерения, които вероятно влияят върху представянето на групата (1⇓⇓⇓⇓–6). В тази статия ние се фокусираме върху важно, но емпирично недостатъчно проучено измерение на задачите, сложността, която обикновено се разбира, че зависи от поне два фактора: (i) броя на отделните компоненти, които съставляват задача и (ii) броя, силата и конфигурация на взаимозависимостите между тези компоненти (7⇓⇓⇓–11).
Интуитивно, сложността на задачата е от очевидно значение за представянето на групата. При други равни условия може да се очаква, че решаващите проблеми ще се представят по-зле при задачи, които имат повече компоненти или за които взаимодействията между компонентите са по-плътни. Освен това може да се очаква сложността на задачата да повлияе на груповата „синергия“, дефинирана като представяне, надвишаващо това, което би се очаквало за съвкупност от хора с подобен размер, работещи независимо – известна още като „номинална група“ (12). В този случай обаче е по-малко очевидно каква би била посоката на ефекта. От една страна, взаимодействащите групи могат да се представят по-добре в сравнение с номиналните групи при сложни задачи, защото са в състояние да разпределят усилията (13), да споделят информация за висококачествени решения (14) или да коригират грешки (15). От друга страна, при по-сложни задачи, взаимодействащите групи могат да изпитат още по-големи загуби в процесите – включително социално ленене (16), групово мислене (17) и междуличностни конфликти (4) – вероятно защото сложните задачи поставят по-големи изисквания към отделните участници и предлагат повече възможности да се забиете в глобално неоптимални местни оптимуми, всеки от които също може да доведе до повишен стрес и недостатъчно представяне спрямо номиналните групи.
Основно предизвикателство пред разрешаването на въпроси относно ефектите от сложността на задачата е, че докато концепцията на високо ниво изглежда интуитивна, тя все още не е операционализирана достатъчно точно, за да позволи на изследователите да определят количествено сложността на различни видове задачи и следователно да правят ябълки към ябълки сравнения между тях. По-скоро съществуващите операционализации често сами по себе си са сложни. Например, един модел изброява 27 фактора, допринасящи за сложността, групирани под 10 измерения на сложността (9), докато други модели са достатъчно специфични за домейн, така че числовите разлики между различните типове задачи са трудни за тълкуване (7). Добавяйки объркване, някои дефиниции подчертават обективната сложност, отнасяйки се само до характеристиките на задачата, които могат да бъдат измерени независимо от тези, които изпълняват задача, докато други подчертават субективната сложност, сложността на задачата, изпитана от тези, които я изпълняват (9, 11).
Тук избягваме тези аналитични трудности, като идентифицираме клас от задачи, чиято сложност може да се променя систематично, като същевременно поддържаме всички останали елементи на задачата фиксирани. По този начин можем лесно да измерим производителността като функция на нарастващата сложност, без да се тревожим за обърквания, произтичащи от други аспекти на задачата, като например тип задача (3) или други характеристики на групови процеси (4, 18). В допълнение, ние изискваме нашите задачи да могат реалистично да се изпълняват независимо или съвместно, като по този начин позволяват директно сравнение между номинални и взаимодействащи групи.
Клас от задачи, които отговарят на тези критерии, са проблеми с удовлетворяването на ограниченията и оптимизацията (CSOP), които се изучават широко в областта на изкуствения интелект и оперативните изследвания. Връзката с оперативните изследвания е полезна, защото за разлика от други проблеми „играчки“, CSOPs картографират по сравнително интуитивен начин набор от практически проблеми с разпределението на ресурсите и са били използвани за моделиране на много проблеми, които са от практически интерес. Примери за CSOPs включват софтуерни проекти за набиране на персонал, където има няколко потенциални задачи от разработчици към дейности за оценка (19); формиране на учебни групи въз основа на критерии, свързани с целите на сътрудничеството (20); железопътно разписание (21); и разпределяне на ваксини, вентилатори и медицински консумативи по време на пандемията от COVID-19 (22). Освен това, докато CSOP улавят важни характеристики на упражненията за групово решаване на проблеми в реалния свят, те не изискват от участниците да имат специализирани умения. В резултат на това участниците могат да бъдат набирани от онлайн услуги, намалявайки разходите и трудността при координиране на едновременното участие на групи. И накрая, както при други сложни проблеми (14, 23⇓–25), функцията за изплащане за CSOP може да се опише като неравен пейзаж на ефективността, където всяка точка от пейзажа представлява комбинация от потенциално взаимозависими избори (решение на проблема) , докато височината на точката представлява ефективността на тази комбинация (26, 27). Следователно CSOPs могат да се характеризират с няколко локално оптимални, но глобално неоптимални решения (26, 27) и така са податливи на потенциално много стратегии и стилове на решение, без нито една универсално превъзходна стратегия (28).
Специфичният CSOP, който проучихме, е проблем за разпределяне на стаи, при който участниците – или като индивидуалисти, или в групи – разпределят N студенти в M стаи, където всеки ученик има определена помощ за всяка стая (SI Приложение, раздел 1.1). Целта на задачата е да се увеличи максимално общата полезност за учениците, като същевременно се спазват ограниченията на Q (напр. „Студенти A и J не могат да споделят една стая или да са в съседни стаи“). Когато задачата се изпълнява в групи, на участниците е разрешено да комуникират чрез текстов чат и да преместват различни ученици едновременно, като по този начин извършват паралелна обработка, ако решат. Критично за нашите цели, сложността на задачите може да се променя систематично чрез коригиране само на три ключови параметъра: броя на учениците , броя на стаите и броя на ограниченията . Наистина, значително предимство на тази задача (и CSOP като цяло) пред задачите, които се изучават по-често в настройките на груповата производителност, е, че нейната сложност може да бъде количествено определена по отношение на времето за изпълнение, необходимо на алгоритмичен решаващ инструмент, за да намери оптималното решение, което позволява за лесно класиране на екземпляри на задачи по сложност (вижте Материали и методи за повече подробности). Фигура 1 илюстрира как сложността може да варира между два екземпляра на проблема със задаване на стая. В случай с ниска сложност, шестима студенти трябва да бъдат разпределени в четири стаи, подчинени само на две ограничения („B и E трябва да са съседи“ и „C и F не могат да живеят в една стая“). В случай с висока сложност, 18 студенти трябва да бъдат разпределени в 8 стаи, предмет на 18 ограничения.
Илюстрация на задачата за назначаване на стая. Задачата изисква разпределяне на N студенти в M стаи, така че да се увеличи максимално общата полезност на студентите, всеки от които има определена полезност за всяка стая, като същевременно се спазват Q ограниченията. Сложността на задачата се характеризира с броя студенти, които ще бъдат назначени , броя на наличните общежития и броя на ограниченията . (Отгоре) Случай с ниска сложност, при който шестима студенти трябва да бъдат разпределени в четири стаи при две ограничения. (Отдолу) Случай с висока сложност, при който 18 студенти трябва да бъдат разпределени в 8 стаи при 18 ограничения. Вижте SI Приложение, раздел S1.1, за подробности и SI Приложение, Фиг. S1–S2, за екранни снимки на интерфейса на задачите.
Дизайн на експеримента
В тази статия тестваме хипотезата, че сложността на задачата намалява относителното представяне на групово срещу индивидуално решаване на проблеми. За тази цел разглеждаме следния въпрос: как балансът между загубите на процеса и синергичните печалби във взаимодействащите групи зависи от сложността на задачата?
Нашият експеримент протече в две фази. Във фаза 1 1200 участници поотделно изпълниха пет задачи за разпределяне на стаи: три задачи с много ниска и две задачи с умерена сложност (SI приложение, таблица S1), както и стандартен тест за четене на ума в очите (SI приложение, раздел S1.2 и Фиг. S3), който обикновено се използва като мярка за социална възприятие и е използван от няколко скорошни проучвания, свързващи социалната възприятие с груповото представяне (18, 29⇓⇓–32).
След завършване на фаза 1, ние оценихме всички участници по ниво на умения и социална възприятие, така че да можем да ги разпределим към експериментални блокове във фаза 2 (Приложение към SI, раздел 1.4 и Фиг. S4). Като отчитаме тези характеристики в нашата процедура за блокова рандомизация във фаза 2, бихме могли да гарантираме, че различните нива на умения и социална възприемчивост (и комбинации от тях) са балансирани в груповите и индивидуалните работни условия. Основната цел на схемата за блокова рандомизация беше да се вземат свръхизвадки от статистически по-рядко срещани комбинации (напр. всички членове на групата с високи умения или висока социална възприемчивост), като по този начин се увеличи статистическата мощност на нашите експерименти. Отбелязваме, че фокусът ни тук е върху сравнението между взаимодействащи и номинални групи, а не върху разликите в състава между взаимодействащите групи; по този начин нашият анализ на ефектите от нивото на уменията и социалното възприятие върху представянето ще бъде публикуван другаде (съгласно нашата предварителна регистрация).
Същите 1200 участници бяха поканени да участват във фаза 2, а първите 828 участници, които се появиха и преминаха проверките за внимание (съгласно нашата предварителна регистрация; вижте SI Приложение, Таблица S2, за размерите на извадката) бяха назначени на втори последователност от пет задачи за разпределяне на стаи (последователността от задачи беше рандомизирана), също с различна сложност (много ниска, ниска, умерена, висока и много висока; SI Приложение, Таблица S3 и Фиг. S5). Всички задачи изтекоха на 10 минути във фаза 2, независимо от сложността. Въз основа на уменията и социалната възприемчивост на всеки участник, измерени във фаза 1, първо разпределихме всеки индивид в блокове (напр. високо умение, висока социална възприятие; смесени умения, висока социална възприятие и т.н.). След това, в рамките на всеки блок, участниците бяха рандомизирани на едно от двете условия: състояние на взаимодействаща група ( участници, формиращи 197 групи с размер 3; данните за 1 група са непълни, което води до броя валидни взаимодействащи групи са 196), в които членовете на групата решават проблема колективно и могат да комуникират помежду си чрез текстов чат; и независимо индивидуално условие ( участници; данните от 3 лица са непълни, което води до броя на валидните независими лица 234), при което всеки участник работи сам върху възложената му задача. Всички резултати, представени тук, са от фаза 2 на експеримента.
Оценка на ефективността.
Във фаза 2 използвахме три показателя за улавяне на производителността в екземпляр на задача за присвояване на стая: (1) нормализиран резултат, дефиниран като действителния резултат, получен в екземпляр на задача, разделен на максималния възможен резултат за тази задача; (2) продължителност (или време до завършване), дефинирана като времето, изминало от началото на задачата до изпращането на решение (или до времето за изчакване на задачата при 10 минути); и накрая, (3) ефективност, дефинирана като нормализиран резултат, разделен на продължителността.
И трите показателя са естествени индикатори за ефективност, които може да пожелаете да оптимизирате при определени обстоятелства. При липса на времеви ограничения, например, нормализираният резултат е очевидна мярка за качеството на решението. Обратно, продължителността е подходяща, когато времето за решаване на проблема е по-важно от качеството (напр. бързо изготвяне на сравнително добър план за разпределение на ресурсите при реакция при бедствие), а ефективността е подходяща, когато и качеството, и бързината са важни (напр. , в разработването на продукта).
След предишна работа (12, 33⇓⇓⇓–37), ние оценяваме представянето на групата в сравнение с така наречените номинални групи, дефинирани като колекция от автономни индивиди с подобен размер. Номиналните групи осигуряват полезен показател за взаимодействащи групи, тъй като те отчитат различната наличност на ресурси между групи и индивиди (12); тоест, те се коригират спрямо количеството интелектуални ресурси, които групите биха могли да използват (т.е. работни часове) и математическата вероятност поне един член да е постигнал същото представяне. По този начин ефективността на взаимодействащата група над тази на номинална група може да се припише на груповото взаимодействие, а не на по-големите ресурси.
Като цяло сравненията между взаимодействащи групи и номинални групи с еквивалентен размер са открили смесени доказателства за синергични ефекти (12): докато взаимодействащите групи често превъзхождат средния член на номинална група (слаба синергия), те рядко превъзхождат най-добрия член ( силна синергия). Отразявайки това разграничение, ние сравняваме нашите взаимодействащи групи с четири показателя за ефективност, всеки от които съответства на отделна номинална група, конструирана чрез изтегляне на трима индивида на случаен принцип и без замяна от същия блок. Първият бенчмарк съответства на резултата за ефективност за произволно избран член на номиналната група (еквивалентен на среден индивид), докато останалите три съответстват на индивида с най-добро представяне във фаза 1 по всеки от трите показателя, дефинирани по-горе (т.е. най-висок резултат, най-ниска продължителност и най-висока ефективност). Следователно номиналните групи симулират ситуация, в която мениджърът възлага работата или на случаен индивид, на индивида с най-висок резултат, на най-бързия индивид или на най-ефективния индивид, според оценката на минало представяне (т.е. резултати от фаза 1, продължителности , и ефективност).
Резултати
Ефективността като функция от сложността на задачата.
Фиг. 2 показва как производителността варира като функция на сложността на задачата. Във всички условия по-високата сложност на задачата доведе до по-ниски нормализирани резултати (Фиг. 2A), по-голяма продължителност (Фиг. 2B) и следователно по-ниска ефективност (Фиг. 2C). Тези тенденции в ефективността също се запазват, когато се измерват отделно за взаимодействащи и номинални групи (SI приложение, раздел S2 и фиг. S7). Средно индивидите и групите прекарват приблизително три пъти повече време на най-сложната задача, отколкото на най-малко сложната задача, но получават нормализирани резултати, които са с приблизително 10 процентни пункта по-ниски. Като се има предвид, че нормализираните резултати бяха почти винаги над 80, тази последна разлика представлява приблизително 50% от ефективния диапазон - голям ефект. Ясната монотонна зависимост на трите мерки за изпълнение от сложността е важна по две причини. Първо, той валидира нашия дизайн, демонстрирайки, че увеличенията на сложността, уловени от промените в параметрите на задачата N, M и Q, се превеждат по ясен начин в сложността, изпитана от нашите участници. Второ, предлага значителен лост за тестване на нашата прогноза, че относителното представяне на взаимодействащи групи спрямо номиналните групи зависи от сложността на задачата.
Промяна на сложността на задачата за разпределяне на стаята. Увеличаването на сложността на задачата (A) намалява нормализирания резултат, (B) увеличава времето, необходимо за изпълнение на задачата, и (C) намалява ефективността. Данните се комбинират за индивидуални и групови условия във всичките шест блока. Лентите за грешки показват 95% доверителни интервали (някои не са достатъчно големи за показване). Групи и индивиди са постигнали поне 80% от максималния резултат в над 85% от задачите; следователно, ефективният диапазон за нормализирания резултат (т.е. оста y на A) е между 80 и 100%. Минималното време за изпращане на решение е 1 мин., а максималното 10 мин.; следователно, ефективният диапазон за продължителността (т.е. оста y на B) е между 1 и 10 минути. Разликата в изпитваната трудност между много ниска и много висока сложност е много голяма: средният нормализиран резултат спадна с около 50% от ефективния диапазон от резултати (от приблизително 95 до 85% по ефективна скала от 80 до 100), а средното време се увеличава с 200% (от 2 на 6 минути).
Доказателство за групова синергия.
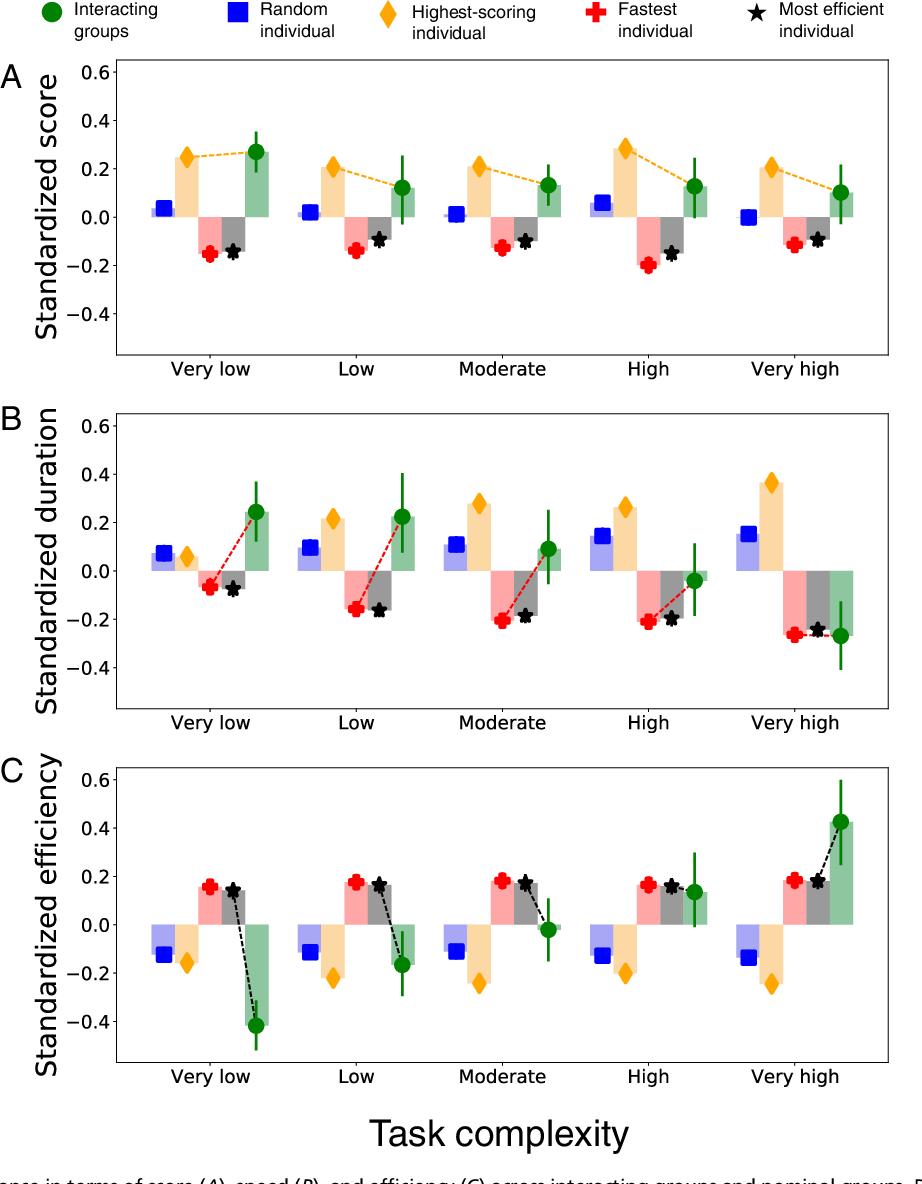
Фиг. 3 сравнява общото стандартизирано групово представяне (трансформирано в z резултати в рамките на всяко ниво на сложност на задачата) с четирите номинални групови дефиниции: случаен индивид, индивид с най-висок резултат, най-бърз индивид и най-ефективен индивид.
Сравняване на ефективността по отношение на резултат (A), скорост (B) и ефективност (C) между взаимодействащи групи и номинални групи. Данните се комбинират във всичките шест блока и се стандартизират (т.е. трансформират се в z резултати) в рамките на всяко ниво на сложност на задачата (разликите са относителни в рамките на нивото на сложност и не трябва да се сравняват между нивата на сложност). Лентите за грешки показват 95% доверителни интервали. Ние повторихме анализите, представени на тази фигура за всеки блок, с качествено сходни резултати (SI приложение, раздел S3 и фигури S8–S10).
Ефективността като качество на решението.
За всички нива на сложност на задачите Фиг. 3A показва, че групите имат по-висок резултат от случайно избраните, най-бързи и най-ефективни членове на еквивалентни по размер номинални групи ( P = 0,013, 95% CI [0,026, 0,225]; P < 0,001, 95% CI [0,184, 0,410]; P < 0,001, 95% CI [0,155, 0,378]; съответно), но по-нисък от този с най-висок резултат член (P = 0,047, 95% CI [−0,159, −0,001]; вижте Приложението SI, Таблици S4–S7, за регресионни таблици). Този резултат е в съответствие с дългогодишни констатации (33⇓⇓⇓–37), че взаимодействащите групи често превъзхождат номиналните групи по отношение на качеството на решението, когато стандартът е зададен от критерий за среден член (слаба синергия), но не и когато е зададен от критерий за най-добър член (силна синергия).
Ефективността като скорост.
Фиг. 3B показва, че взаимодействащите групи изпълняват по-сложни задачи - но не и по-прости - по-бързо от случайните членове и членовете с най-висок резултат на номинални групи с еквивалентен размер. Освен това, взаимодействащите групи са толкова бързи, колкото най-бързите и най-ефективни членове при най-висока сложност на задачите (вижте SI Приложение, таблици S8–S10, за регресионни таблици). Те предполагат, че наистина за задачи с много компоненти (ученици и стаи) и плътни взаимозависимости (много ограничения), ползите от разпределянето на работата на група може да надвишат загубите на процеса, свързани с взаимодействащи групи, което е в съответствие с констатациите в предишна работа ( 36).
Ефективност като ефективност.
Накрая, фиг. 3C показва, че за най-сложните задачи печалбите в скоростта надхвърлят дефицитите в резултата. Това води до поразително взаимодействие между сложността на задачата и организацията на работа: докато взаимодействащите групи са значително по-малко ефективни от избрани членове на номинални групи при прости задачи, тяхната относителна ефективност се увеличава със сложността на задачата, докато не надминат най-високите, най-бързите и най-ефективните членове с най-висока сложност (вижте SI Приложение, Таблици S11–S13, за регресионни таблици). Този резултат напомня на груповото вземане на решения сред социалните насекоми, при което скорошно проучване установи, че колониите от мравки превъзхождат отделните мравки, когато задачата за разграничаване е трудна, но не и когато е лесна (38).
Разопаковане на груповата синергия.
Констатацията, че взаимодействащите си групи са по-ефективни от най-добре подбраните членове на еквивалентни по размер номинални групи – по която и да е от нашите четири дефиниции – когато задачата е сложна, но не когато задачата е проста, предполага, че балансът между загубите на процеса и синергичните печалби наистина зависи от сложността на задачата. За по-добро разбиране на тази зависимост и отбелязване, че промяната в ефективността, видима на (Фиг. 2C), е по-зависима от промяната в продължителността на задачата (която варира средно между 2 и 6 минути, Фиг. 2B), отколкото от промяната в постигнатия резултат (което варира между 95% и 85% средно, фиг. 2A), следва да представим проучвателен анализ на времето, прекарано във всеки етап от решаването на задачата. Този анализ е възможен благодарение на изключително детайлния характер на нашите данни. Тъй като всяко действие, предприето от всеки участник, има клеймо за време, можем да разделим общото време за решение на много точно измерени сегменти, които съответстват на различни етапи от процеса на решаване на проблема. За по-голяма яснота дефинираме четири ключови сегмента, илюстрирани схематично на фиг. 4A:
Крайни етапи на изпълнение на задачата. (A) Четирите основни етапа в процеса на решаване на проблеми: (i) генерира се първото междинно решение, (ii) генерира се най-доброто междинно решение, (iii) генерира се окончателното решение и (iv) крайното решение е подадено. (B, D, F и H) Прекараното време (в минути) от групи и индивиди (независимо дали произволни, с най-висок резултат, най-бързи или най-ефективни) във всеки времеви сегмент. (C, E, G и I) Стандартизираното прекарано време (трансформирано в z резултати; т.е. показващо относителната разлика в рамките на нивото на сложност) във всеки времеви сегмент. Лентите за грешки показват 95% доверителни интервали.
Време до първото решение, .
Времето от началото на задачата до генерирането на първото решение може да се разглежда като време, прекарано във формулиране на стратегия да подходи към задачата.
Време за най-добро решение, .
Най-доброто решение не е непременно изпратеното, тъй като екземплярът на задачата приключва само след като група/индивид реши да изпрати решение и групите/индивидите могат да генерират решения след тяхното най-добро решение, без да се връщат към него.
Време от най-доброто до окончателното решение, .
Времето, прекарано между генерирането на най-доброто и крайното решение, което може да се разглежда като „излишно проучване“, намалява ефективността, тъй като води до по-ниско (или равно) качество на решението, но по-голяма обща продължителност на задачата.
Време от окончателното решение до изпращане, .
Времето, прекарано между генерирането на окончателното решение и вземането на решение за изпращането му, което може да се разглежда като „ време за ангажиране“, може да бъде друг източник на неефективност, тъй като води до еднакво качество на решението, но увеличава общата продължителност на задачата.
Фиг. 4 показва два набора от сравнения между взаимодействащи и номинални групи за всеки от тези четири сегмента. Фиг. 4 B, D, F и H показват необработените продължителности за , , и
Първо, наблюдаваме, че (средно) взаимодействащите групи прекарват по-малко време в (време до първото решение, фиг. 4 B и C), отколкото членовете на номиналните групи, независимо от сложността на задачата ( за всички; и SI Приложение, Таблица S14). Спекулираме, че това наблюдение може да е свързано с аргументи от скорошни проучвания, че членството в група намалява чувството за отговорност и съжаление, с което членовете могат да се сблъскат при едни и същи обстоятелства поотделно. Ако е правилно, намалената емоционална бариера за действие може да бъде основен механизъм, каращ членовете на групата да действат по-рано (39).
Второ, наблюдаваме забележим ефект от сложността на задачата върху (време за най-добро решение, Фиг. 4 D и E): взаимодействащите групи достигат по-бавно до най-доброто си решение от най-бързите и най-ефективните членове на номиналните групи за най-малко сложната задача, но по-бързи за най-сложната задача (P < 0,001, 95% CIs [0,119, 0,385] и [0,109, 0,371], съответно, при най-ниската сложност и P < ; 0,001, 95% CIs [−0,351, −0,085] и [−0,370, −0,108], съответно, при най-високата сложност; вижте таблици S17–S18 в приложението SI за регресионни таблици). Важно е да отбележим, че по-голямата част от продължителността на задачата се изразходва в този сегмент, което предполага, че скоростта на най-доброто решение е основният фактор, допринасящ за груповата синергия. Едно потенциално обяснение защо взаимодействащите групи са по-бързи в намирането на най-доброто решение при висока сложност е, че взаимодействащите групи осъзнават някои ползи от разделението на труда (вижте SI Приложение, раздел S4 и Фигура S11, за подсказващи доказателства). Друго възможно обяснение, за което виждаме някои анекдотични доказателства в чат регистрационните файлове (SI Приложение, Фиг. S11), е, че взаимодействащите групи са по-склонни да задоволят, като приемат налично в момента решение като задоволително (40). Друго може да е, че те се възползват от редуване, при което един човек е предимно активен, докато другите обмислят следващия си ход(и). За съжаление, настоящият дизайн на експеримента не ни позволява да правим разлика между тези алтернативни обяснения, поради което те остават спекулативни.
Трето, наблюдаваме, че независимо от сложността, взаимодействащите групи прекарват повече време в (излишно изследване, Фиг. 4 F и G) сегмент спрямо членовете на номиналните групи; както при , разликата е последователна между нивата на сложност (вижте SI Приложение и таблици S19–S20 за регресионни таблици). Четвърто, взаимодействащите групи също прекарват повече време, за да се ангажират с решение (), отколкото избраните членове на номиналните групи, отново независимо от сложността (Фиг. 4 H и I и SI Приложение, Таблица S14) . Спекулираме, че фактът, че взаимодействащите групи могат да комуникират чрез чат (и липсата на назначен лидер), може да добави натиск върху групите да гарантират, че техните решения се вземат колективно (т.е. постигане на консенсус), което може да допринесе за наблюдавания ефект.
Пето, наблюдаваме, че средната обща продължителност на задачата варира от минути при много ниска сложност до минути при много висока сложност (от максимум 10 минути), което означава, че участниците обикновено изпращат решението и завършват екземпляра на задачата, преди да изтече времето. Това наблюдение е от значение за нашия анализ, тъй като нашите сравнения на ефективността на взаимодействащи групи с тези на избрани членове на номинални групи не се повлияват от ограничението във времето.
Обобщавайки, Фиг. 4 разкрива два вида загуби на процеса (т.е. допълнителното време, прекарано в излишно проучване и постигане на консенсус) и два типа синергии (т.е. по-бързо време до първо решение и по-бързо време до най-доброто решение за сложни задачи ). Интересното е, че докато синергиите - по-специално във времето за най-добро решение - зависят от сложността на задачата, загубите в процеса не го правят. С други думи, нашите констатации предполагат, че присъствието във взаимодействаща група има фиксирани разходи, които са относително последователни в нивата на сложност на задачата, но полза, която варира в зависимост от нивата на сложност (т.е. по-малко време, изразходвано за намиране на най-доброто решение).
За по-нататъшно изясняване на тази констатация, ние след това събираме разходите и ползите, за да определим количествено стойността на изпълнението на задачата във взаимодействаща група на различни нива на сложност. По-специално, ние измерваме всеки разход и полза като абсолютната разлика, по отношение на изразходваното време, между взаимодействащи групи и случаен (т.е. среден) член на номинални групи във всеки времеви сегмент:
Фиг. 5 показва, че общите разходи, свързани с неефективността на взаимодействащата група (т.е. прекомерно проучване, постигане на консенсус) надхвърлят синергичните ползи (т.е. печалби от скоростта при намиране на най-доброто решение) при решаване на задачи с ниска сложност, но не и на такива с висока сложност. Това обяснява нашето откритие, че групите са по-ефективни от членовете с най-висок резултат, най-бързите и най-ефективните членове на номинални групи с еквивалентен размер, когато задачата е сложна, но че тази връзка е обърната, когато задачата е проста. Откриваме подобни резултати за сравнението на член с най-висок резултат (Приложение SI, раздел S5 и Фигура S12).
Разходи-ползи от взаимодействащи групи. Фигурата илюстрира абсолютната разлика по отношение на средното време, прекарано между взаимодействащи групи и средна индивидуална номинална група във всеки времеви сегмент.
Проучване на разликите в подходите за решаване на проблеми.
Като обобщим нашите основни резултати, взаимодействащите групи са по-ефективни дори от най-ефективния член на номинални групи за проблеми с висока сложност; следователно заключаваме, че те показват силна синергия за ефективност (фиг. 3C). По отношение на скоростта, взаимодействащите групи са по-бързи от средния (случайно избран) член и толкова бърз, колкото най-бързият член на номинални групи с еквивалентен размер (фиг. 3B), като по този начин показват само слаба синергия. Що се отнася до качеството на решението, взаимодействащите групи показват още по-слаба синергия, тъй като имат по-висок резултат от средния член, но не толкова добре, колкото членът с най-висок резултат от номиналните групи (фиг. 3A).
За по-нататъшно проучване на тези резултати, ние проучихме броя и скоростта на генерираните междинни решения, където междинно решение се дефинира като разпределяне на студенти в стаи (т.е. всяко действие, предприето от участник, генерира междинно решение). Както е показано на Фиг. 6 A и B, наблюдаваме, че групите не само генерират повече междинни решения от произволните, с най-висок резултат, най-бързи и най-ефективни членове на номинални групи с еквивалентен размер ( за всички, 95% CI , , и съответно; SI Приложение, Таблица S23); направиха го и с по-висок процент ( за всички, 95% CI , , и , съответно; SI Приложение, Таблица S23). Взаимодействащите групи също показват по-широк радиус на решение, дефиниран като максималното разстояние за редактиране (т.е. броя на разликите в разпределенията на студенти/стаи) между първото цялостно решение (т.е. всички студенти, разпределени в стаи, но конфликтите може да са неразрешени) и всички следващи цялостни решения, което предполага, че са изследвали пространството на решенията по-широко (фиг. 6C; за всички, 95% CI , , и съответно; SI Приложение, Таблица S23). Също така потвърдихме това качествено заключение, използвайки две други мерки за изследване: процентът на решенията в рамките на разстояние за редактиране от две от крайното решение и процентът на междинните решения, които включват нарушение на ограничението (SI Приложение, Фигури S13 и S14).
Механични разлики в подходите за решаване на проблеми между взаимодействащи групи и индивиди. Взаимодействащите групи генерират (A) повече решения, (B) с по-бърза скорост и (C) изследват пространството за решения по-широко. (D) Въпреки това, качеството на най-доброто намерено решение (независимо дали е изпратено или не) не е по-добро от решението, намерено от индивидуалните номинални групи с най-висок резултат. Лентите за грешки показват 95% доверителни интервали.
В светлината на тези наблюдения е още по-изненадващо, че взаимодействащите групи не са намерили решения с по-високо качество от члена с най-висок резултат от номиналните групи (фиг. 6D; ; SI Приложение, Таблица S23). Отчасти разликата може да се обясни с това, че взаимодействащите групи също не успяват да изпратят своето най-добро намерено решение с по-висок процент от индивида с най-висок резултат: при всички сложности индивидът с най-висок резултат не успява да изпрати най-доброто си решение от времето, докато взаимодействащите групи не успяват да представят най-добрите си решения от времето (; разлика в пропорциите). В резултат на това представените решения от взаимодействащи групи бяха по-лоши в сравнение с индивидуалните членове с най-висок резултат, отколкото ако всеки беше изпратил своето най-добро намерено решение (сравнете Фиг. 3A с Фиг. 6D), въпреки че дори тогава остава известна празнина.
Какво може да обясни комбинацията от силна синергия в ефективността и само слаба синергия за качество и скорост на решението? Предишни изследвания, които концептуализират решаването на проблеми като адаптивно търсене в неравен пейзаж на производителността (14, 27), при който всяка точка от пейзажа представлява едно решение на заданието на стаята, а височината на точката представлява изпълнението на това задание, осигурява няколко, възможно взаимосвързани обяснения. Едно потенциално обяснение е, че хората с най-висок резултат имат по-добро представяне (приближения с по-ниско измерение) на реалния пейзаж на ефективността, което им позволява да оценяват решения (и траектории на решение) офлайн, без да ги тестват чрез експерименти (41, 42). По-добрите представяния могат да доведат до по-точни офлайн оценки и по-ефективни усилия за търсене (26, 43, 44), характеризиращи се с по-малко междинни решения и по-високо качество на решението. Като алтернатива, групи от решаващи проблеми може да имат противоречиви интереси (напр. максимизиране на резултата срещу минимизиране на продължителността) и, следователно, различни визии за правилния курс на действие (45). Ако е вярно, групите могат да се възползват от централната координация чрез назначаване на лидер на група (45) или от интервенции, свързани с процеса, като налагане на периодични прекъсвания във взаимодействието (46, 47). Още една възможност е, че когато времето е ограничено, стратегиите за търсене, които позволяват бързи печалби (т.е. рязко подобрение на производителността в началото) и намаляват обема на проучване, може да изглеждат по-добри (26). Следователно, докато стратегията за локално търсене за задълбочаване на пътя (напр. изкачване на хълм), възприета от членовете с най-висок резултат от номинални групи с еквивалентен размер, може да осигури краткосрочни ползи за ефективността, стратегията на взаимодействащите групи за разширяване на домейна за търсене може да бъде по-изгодна в дългосрочен план (48, 49).
Дискусия
За много задачи, представляващи интерес, мениджърите могат да решат дали да възложат задача на взаимодействаща група или на сравним брой лица, работещи независимо (12). За настройки като тези нашите резултати предлагат няколко прозрения. Първо, решенията за това как да се разпредели работата - на взаимодействащи групи или на номинални групи - трябва да зависят от сложността на задачата и начина, по който се оценява изпълнението. Например, ако мениджър иска да намери работещо решение за CSOP за най-малко време, препоръката би била да помолите група да реши проблема, когато проблемът е сложен, но да помолите независими решаващи проблеми, когато е прост. Трябва да се отбележи, че резултатите от продължителността и ефективността, представени тук, всъщност могат да подценят как това ще работи на практика. Например, ако работата беше организирана в номинални групи, тази подредба пак щеше да доведе до множество различни решения, между които някой мениджър да избира. Въпреки че нашата операционализация на номинални групи симулира ситуация, в която мениджърът взема решение мигновено, има обстоятелства, при които мениджърът може да иска да разгледа достойнствата на различните решения и това ще отнеме различно от нула време. Това не е случаят с взаимодействащите групи, където процесът на вземане на решение вече е включен в изминалото време на упражнението за решаване на проблеми.
Второ, нашите констатации също предполагат, че възможно обяснение защо загубите от групови процеси са залегнали по-видно място в резултатите от изследванията, отколкото синергичните печалби (12), е, че лабораторните изследвания на груповата ефективност обикновено разчитат на много прости задачи. Наистина, най-ясните лабораторни доказателства до момента за превъзходно групово представяне, макар и рядко, идват от групи, работещи върху относително сложни задачи (13, 46, 50, 51); Въпреки това, фактът, че сложността на задачите не се променя систематично в рамките на едно проучване, представлява основен източник на неконтролирани вариации в минали изследвания (17, 36).
Трето, нашият анализ на това как взаимодействащите групи и независимите индивиди се различават по времето, което прекарват по време на различни части от процеса на решаване на проблеми, предлага представа за това как груповите процеси могат да бъдат подобрени. Например, нашата констатация, че групите прекарват повече време, за да решат, че дадена задача е изпълнена (т.е. постигане на консенсус), предполага, че назначаването на лидер на група със способността едностранно да вземе това решение, както прави индивидът, трябва да намали този източник на забавяне , като по този начин подобрява ефективността на групата. Нещо повече, нашата констатация, че е по-малко вероятно взаимодействащите групи да изпратят своето най-добро намерено решение предполага, че съхраняването на техните най-добри решения, така че да могат да бъдат презареждани и потенциално модифицирани в следващите стъпки (повсеместна функция на софтуера за лична продуктивност) също трябва да подобри тяхната производителност ( 46).
Четвърто, нашият анализ на динамиката на решенията на групи срещу индивиди провокира допълнителни пъзели за бъдеща работа. По-специално, ако групите генерират повече решения по-бързо и по-ефективно в по-широк диапазон от пространството за решения, отколкото дори индивидите с най-висок резултат, защо те не намират по-добри решения?
Накрая заключаваме, че науката за груповото представяне би се възползвала от по-задълбочено, по-систематично оценяване на приликите и разликите между задачите, които групите трябва да изпълняват, както в лабораторията, така и на място. Има нужда от всеобхватна, емпирично обоснована теория за груповите задачи (12). Изследователска програма, която систематично променя видовете задачи заедно с позволените групови процеси и други контекстуални фактори, би развила основната наука за групово решаване на проблеми, като същевременно се занимава с практически приложения.
Материали и методи
Проучването беше прегледано от Консултативния съвет по етика на изследванията на Microsoft и одобрено от Съвета за институционален преглед на изследванията на Microsoft (MSR IRB; одобрение 0000019). Всички участници предоставиха изрично съгласие за участие в това проучване и MSR IRB одобри процедурата за съгласие. Нашият експериментален дизайн, размер на извадката и анализи, сравняващи ефективността на взаимодействащи групи и номинални групи, бяха предварително регистрирани преди събирането на данните (AsPredicted 13123). Всички останали анализи са проучвателни.
Алгоритмично решаване.
Ние моделирахме всеки проблем със задаване на стая като програмен проблем със смесено цяло число и генерирахме времето за изпълнение на компютрите за решаване на всеки проблем с помощта на софтуера IBM ILOG CPLEX Optimization Studio, който е високопроизводителна програма за решаване на математическо програмиране за линейно програмиране, програмиране със смесени цели числа и квадратично програмиране. Софтуерът работи на лаптоп с микропроцесор Intel Core i5, работещ на скорост от 2,6 GHz. Изпълнихме софтуера, използвайки конфигурацията на параметрите по подразбиране. Единицата на времето за изпълнение във файла на задачите е „ticks“, което е единицата на CPLEX за измерване на количеството извършена работа. Съответствието между тиковете и времето на часовника варира в зависимост от платформите (включително хардуер, софтуер, натоварване на машината и т.н.), но като се има предвид програмен проблем със смесено цяло число и настройките на параметрите, тиковете, необходими за решаване на проблем, са детерминистични. В този смисъл надеждността на тест-повторен тест на алгоритмичния решаващ проблем е 1. Вижте Приложението SI, раздел 1.4.2, за допълнителни подробности.
Статистически анализ.
Тъй като всяка взаимодействаща група (или индивид) изпълни петте задачи за разпределяне на стаите, ние проведохме тестове за разлики между условията на ниво задача. За ефектите на взаимодействие моделирахме данните, използвайки обобщен линеен смесен модел за всеки резултат (напр. резултат, продължителност и ефективност) със случаен ефект за груповия или индивидуалния идентификатор. Тези модели отчитат вложената структура на данните. Всички статистически тестове бяха двустранни (според нашата предварителна регистрация). Подробности за статистическите тестове са в Приложение SI, раздел S7.
Стандартизирани коефициенти.
За да позволим смислени сравнения на размерите на ефектите между задачи с различни нива на сложност, ние стандартизираме различни показатели за ефективност (напр. резултат, продължителност, ефективност и брой решения) в рамките на всяко ниво на сложност. Например стандартизираната стойност на измерването X, измерена за екземпляр на задача i със сложност c, се определя катокъдето
Наличност на данни
Данните и кодът за репликация са налични в Harvard Dataverse, https://doi.org/10.7910/DVN/RP2OCY (52). Експериментът е разработен с помощта на платформата Empirica (53). Изходният код за задачата за присвояване на стая може да бъде намерен на https://github.com/amaatouq/room-assignment-csop, а изходният код за теста „Четене на ума в очите“ може да бъде намерен на https://github .com/amaatouq/rme-test.
Благодарности
Благодарим на Валери Якубович, Хажир Рахмандад и Джеймс Хотън за техните полезни дискусии и отзиви. Авторите изказват своята благодарност на Фондация Алфред П. Слоун (G-2020-13924) за финансовата подкрепа.
Бележки под линия
Принос на автора: A.A., M.Y. и D.J.W. проектирани изследвания; A.A., M.Y. и D.J.W. извършени изследвания; A.A., M.A., M.Y. и D.J.W. допринесе с нови реактиви/аналитични инструменти; A.A., M.A., M.Y. и D.J.W. анализирани данни; и A.A., M.A., M.Y. и D.J.W. написа хартията.
Авторите декларират липса на конкурентен интерес.
Тази статия е пряко подаване на PNAS.
Тази статия съдържа поддържаща информация онлайн на https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2101062118/-/DCSupplemental.
Тази статия със свободен достъп се разпространява под лиценз Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 (CC BY-NC-ND).




